The past few sections have been devoted mainly to the generalization of the previously rather strict notion of class. In this section we find the culmination of this tendency, in the complete abandoning of class as a relevant flexagon characteristic.
We have seen that face degree is determined by class, and that is all. Thus, where the hinges between two leaves are placed in relation to the other hinges to those leaves makes no difference whatsoever in the shape of the map. Nor, for that matter, does the shape or size of the leaves involved. Any variation in this direction has been shown acceptable; any shape of plan may be assembled into a flexagon with any given kind of map, so long as the hinging - or, what is equivalent, the numbering of the leaves is done correctly. Let us, then, make the shapes and sizes of the leaves completely arbitrary, irrelevant. This is difficult to do in practice, so we make use of the fact that hinging and numbering are equivalent by using one in place of the other. Using numbering only gives a ``plan'' made up of separate leaves, to be arranged in specified order, and to be rearranged only by the allowed operations: flexing, rotating, etc. The hinging is left to the imagination of the operator. What is the class of this flexagon? As first proposed, the class makes no difference at all (within limits: if the ``class'' is ``lead plates 10 ft. square'', practical difficulties may arise in performing the various operations). For the sake of convenience, we may use a set of rectangular cards, numbered on both sides. Also we may limit ourselves to one unit per flexagon, since the flexagon no longer has angles meeting at a center. If desired, a holder (which fixes the constant cyclic order) may be made for the cards, so that they are not rearranged by accident.
Now that we have a general idea of what the ``cards'' look like, we must learn to operate with them. This will be slightly more difficult than it was in flexagons where there were hinges to serve as guides, but it will also demonstrate far more clearly the nature of each operation. First we notice that all the cards actually do is give us a rearrangeable ordered set of ordered number pairs. Thus we can easily represent all the essential details of a card flexagon by a sequence of numbers. This may bring to mind the flexagon representation of C. O. Oakley and R. J. Wisner (see section 4) and the temptation to call the number sequence the flexagon, the object itself a ``flexagon model''. As far as the present authors are concerned, the two are equivalent.
As for the numbers actually used on the cards, it must be recalled that there are several systems for labelling flexagons, all of then acceptable: the number sequence, constant order, and pat structure systems.
The first of these, the number sequence system, results in a set of cards
labeled with the numbers
![]() and arranged so that like numbers are together, in the order shown above,
but with the cycle broken in two spots to form a pair of pats. (All the
card sequences such as the one above, must be considered cyclic: the first
term is understood to follow the last.) The trouble with this system is that
any two flexagons of order
and arranged so that like numbers are together, in the order shown above,
but with the cycle broken in two spots to form a pair of pats. (All the
card sequences such as the one above, must be considered cyclic: the first
term is understood to follow the last.) The trouble with this system is that
any two flexagons of order ![]() are indistinguishable unless further
information is given.
If we are given the map, we can follow it in operating
the flexagon, but we would prefer to be independent of the map.
are indistinguishable unless further
information is given.
If we are given the map, we can follow it in operating
the flexagon, but we would prefer to be independent of the map.
The constant order system incorporates all the information given by
the map into the cards. To construct a constant order card flexagon, the
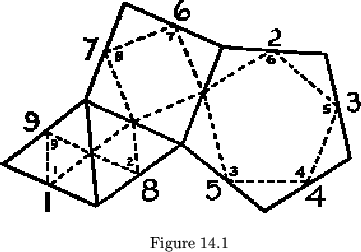
outer faces in the map are numbered in the order in which they are approached
by the traversal of the hinge network (large numbers in fig. 14.1).
This establishes a correspondence between this system of numbering
and the number sequence numbering system. To change system, we can
now easily substitute the numbers of the constant order into the positions
of the terms of the corresponding number sequence cards. The card flexagon
for fig. 14.1 would be
![]() ,
again broken into two pats. As can be seen, all the process really
amounts to is the copying down of the constant order numbers from about the
edge of the map. Since in both the constant order and the number sequence
systems adjacent leaves (number pairs) have like numbers facing one another,
we can eliminate one number in each pair and let a leaf be represented by
only one number, with the understanding that the surfaces of two adjacent
leaves that face together are actually to be colored alike (they make up
the same side). Then the flexagon of fig. 14.1 becomes, in constant order
cards,
,
again broken into two pats. As can be seen, all the process really
amounts to is the copying down of the constant order numbers from about the
edge of the map. Since in both the constant order and the number sequence
systems adjacent leaves (number pairs) have like numbers facing one another,
we can eliminate one number in each pair and let a leaf be represented by
only one number, with the understanding that the surfaces of two adjacent
leaves that face together are actually to be colored alike (they make up
the same side). Then the flexagon of fig. 14.1 becomes, in constant order
cards,
![]() and customary flexagons, with hinges,
may be so labeled by simply
numbering the leaves in the plan from 1 to
and customary flexagons, with hinges,
may be so labeled by simply
numbering the leaves in the plan from 1 to ![]() in the order in
which they are attached to one another.
in the order in
which they are attached to one another.
The pat structure system, unlike the other methods, views the flexagon not from the point of view of a fixedly numbered unit of leaves, but as an ordered pair of structures of leaves, We have seen (section IV) the relationship between the pat structure system and the constant order system in triflexagons; it is analogous in the general case.
Our next problem is to interpret the flexagon operations in terms of operations upon the sequences of numbers that we have obtained. The simplest of these is rotation, which reverses the order of the two pats, without altering them structurally. Turning over the flexagon inverts the structure of each pat, without reversing their order. These operations can be clearly interpreted in all the systems. All remaining operations involve alteration of the pat structure. Of these other operations, which include distorting, flexing, and any other operations that one should choose to allow, only flexing will be considered here.
In describing a flex, the first thing to notice is that it acts upon
three sets of leaves, each of which may or may not change pats, may be
inverted, etc.,
but is not broken up. One of these sets is an entire pat;
the other two make up the second pat, and are separated by a thumbhole.
To recognize a thumbhole, we notice that it must be any spot at which the
leaves above, connected to another pat along one edge of the given pat, are
connected to the leaves below, which connect to another pat along a
different edge of the given pat, by a single hinge. For this to be the case,
the leaves in the pat must be divided by the thumbhole into two sets of
leaves, each of which is made up of leaves lying together in the plan. Here
we find our relationship to the constant order system, for this means that
one must be able to arrange all the numbers between the thumbholes in each
pat consecutively. There will be just ![]() thumbholes per cycle, not
including the two thumbholes separating the two pats in each unit. The fact
that pats must be separated by thumbholes lets us know which groupings of
leaves are possible as faces.
thumbholes per cycle, not
including the two thumbholes separating the two pats in each unit. The fact
that pats must be separated by thumbholes lets us know which groupings of
leaves are possible as faces.
Now, flexing is the operation which folds together two pats, thus
forming a ![]() st thumbhole, and then removes a different thumbhole,
so that the face is changed. The critical position is that at which
there are
st thumbhole, and then removes a different thumbhole,
so that the face is changed. The critical position is that at which
there are ![]() thumbholes, in the folded-together unit. We must first
know which of the sides is to be folded together; where the extra
thumbhole is to be formed. The formation of this thumbhole will eliminate
any thumbholes that might be present from another cycle. Then we
pick any one of the
thumbholes, in the folded-together unit. We must first
know which of the sides is to be folded together; where the extra
thumbhole is to be formed. The formation of this thumbhole will eliminate
any thumbholes that might be present from another cycle. Then we
pick any one of the ![]() thumbholes remaining of the thumbholes previously
present, in the folded together unit, and using this, lay the flexagon
flat again. The reason why the thumbholes must now be thought of in
terms of the folded-together unit, or in terms of a single cycle, is
that in flexagons of
thumbholes remaining of the thumbholes previously
present, in the folded together unit, and using this, lay the flexagon
flat again. The reason why the thumbholes must now be thought of in
terms of the folded-together unit, or in terms of a single cycle, is
that in flexagons of ![]() there will be a mixture of left -and right-
flexes, so that thumbholes of other cycles cannot be separated by assigning
them all to, say, the left-hand pat, as we did in triflexagons.
However, there is one difficulty in finding which of the thumbholes remain
in the folded-together unit. Since the flexagon plan is cyclic
in structure, we have no way of knowing the order of the two pats, unless
we invent some way of distinguishing the two different hinges joining
the two pats. If we cannot distinguish these hinges, we will be unable
to tell which of the spaces between two pats has become a thumbhole
when the flexagon has been folded together, and, if the ambiguity persists,
the folded together structure will be divisible into thumbholes
at any point, due to the flexagons cyclic construction. To prevent this
we say that the hinge between the highest-numbered leaf in the left-hand
pat, as seen written out in numbers, and the lowest-numbered leaf in
the right-hand pat is the hinge that will be folded together to make
the extra thumbhole. That is, the constant order numbers of the right-hand
leaves follow those of the left-hand leaves. In the number sequence
system there is no possible way to tell the thumbholes without a
map, anyway. In the constant order system, the remaining break in the
constant order will sort out the desired thumbholes. To keep in mind that
it is a break in the cyclic constant order, the two leaves connected by
the unfolded-together hinge can be encircled: the lowest term of the
left-hand pat, and the highest term of the right-hand pat. In the pat
structure system, we need merely keep in mind that, in folding together,
the right-hand pat must receive higher numbers than the left-hand pat
in the pat structure of the folded-together unit. Then the pat structure
need not be considered cyclic. Although the method used in the pat
structure system may seem simpler, it does require renumbering of leaves,
and therefore, while well-suited to work with sequences of numbers, is
not well suited to card flexagons.
there will be a mixture of left -and right-
flexes, so that thumbholes of other cycles cannot be separated by assigning
them all to, say, the left-hand pat, as we did in triflexagons.
However, there is one difficulty in finding which of the thumbholes remain
in the folded-together unit. Since the flexagon plan is cyclic
in structure, we have no way of knowing the order of the two pats, unless
we invent some way of distinguishing the two different hinges joining
the two pats. If we cannot distinguish these hinges, we will be unable
to tell which of the spaces between two pats has become a thumbhole
when the flexagon has been folded together, and, if the ambiguity persists,
the folded together structure will be divisible into thumbholes
at any point, due to the flexagons cyclic construction. To prevent this
we say that the hinge between the highest-numbered leaf in the left-hand
pat, as seen written out in numbers, and the lowest-numbered leaf in
the right-hand pat is the hinge that will be folded together to make
the extra thumbhole. That is, the constant order numbers of the right-hand
leaves follow those of the left-hand leaves. In the number sequence
system there is no possible way to tell the thumbholes without a
map, anyway. In the constant order system, the remaining break in the
constant order will sort out the desired thumbholes. To keep in mind that
it is a break in the cyclic constant order, the two leaves connected by
the unfolded-together hinge can be encircled: the lowest term of the
left-hand pat, and the highest term of the right-hand pat. In the pat
structure system, we need merely keep in mind that, in folding together,
the right-hand pat must receive higher numbers than the left-hand pat
in the pat structure of the folded-together unit. Then the pat structure
need not be considered cyclic. Although the method used in the pat
structure system may seem simpler, it does require renumbering of leaves,
and therefore, while well-suited to work with sequences of numbers, is
not well suited to card flexagons.
Supposing that we are able to eliminate the thumbholes of any other
cycle, we can set up the actual mechanism of flexing in all three systems.
Suppose that a comma represents a thumbhole, a semicolon the space between
two pats. To represent some specific permutation ![]() of the set of
of the set of ![]() consecutive integers
consecutive integers
![]() , we will use the notation
, we will use the notation
![]() will indicate the permutation
will indicate the permutation
![]() with the terms taken in
reverse order. Then, for the three systems, we have the following, where
with the terms taken in
reverse order. Then, for the three systems, we have the following, where
![]() , the cycle is arbitrary, and all addition is mod
, the cycle is arbitrary, and all addition is mod ![]() .
.