In order to build any flexagon, it is necessary to satisfy enough requirements to specify it completely; these include such classifications as the number of leaves, their shape, arrangement in the plan, and the order in which they are folded together. So far it has been made possible to specify a given flexagon precisely under each of these categories; we now hope to establish more general requirements, to specify general classes of flexagons more broadly.
What sign sequences, in general, will generate flexagons? Two limitations
might occur to us. First, we want the sign sequence to be reducible to the
sequence of a known flexagon. For then this known flexagon could be extended
to give the desired plan. The second rule is that the sum of the signs be
congruent to zero, mod
![]() . However, if we allow flexagons to have
compound faces, this second requirement disappears, and if zero degree faces
are allowed, the first rule will not necessarily take effect. As for the
first rule, it may be simplified considerably by noticing that the only
irreducible sign sequences are of the form
. However, if we allow flexagons to have
compound faces, this second requirement disappears, and if zero degree faces
are allowed, the first rule will not necessarily take effect. As for the
first rule, it may be simplified considerably by noticing that the only
irreducible sign sequences are of the form
![]() , where
, where ![]() is an angle and, in reducing,
adjacent terms are replaced by their sum (mod 360
is an angle and, in reducing,
adjacent terms are replaced by their sum (mod 360![]() ), provided
this sum is non-zero. In fact, these are the only sequences that cannot be
reduced to sequences of the form
), provided
this sum is non-zero. In fact, these are the only sequences that cannot be
reduced to sequences of the form ![]() or
or ![]() ,
, ![]() . Then these flexagons
(except
. Then these flexagons
(except ![]() ,
, ![]() flexagons) are those that must have zero-degree faces.
flexagons) are those that must have zero-degree faces.
Considering only flexagons without zero-degree or compound faces, and of class 3 or 4, we can further specify requirements on the sign sequence. Considering the class 3 flexagons first, notice that all possible equilateral plans may be arranged on a lattice of equilateral triangles (for nonequilateral leaves, the sign sequence works if and only if the corresponding sign sequence for equilateral triangles works). This lattice may be thought of as three interlaced hexagonal lattices (see fig. 15.1).
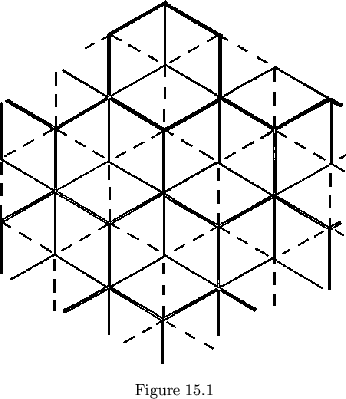
Then the sum of the sign sequence terms will be congruent to zero
(mod 360![]() ) in those plans in which the entering and leaving
hinges lie on edges of the same hexagonal lattice.
The proof of this depends on the fact that passing through any single
hexagon does not change the sign sequence sum. As we see in fig. 15.2,
no matter where we leave the hexagon, the sum of the signs within the
flexagon is zero; passing about the center of the flexagon once
or more does not change the sums. A similar demonstration will give the
corresponding result for tetraflexagons: when the plan is placed on a square
lattice, the incoming and outgoing hinges must be parallel and they must
fall on lines separated by an even number of squares:
) in those plans in which the entering and leaving
hinges lie on edges of the same hexagonal lattice.
The proof of this depends on the fact that passing through any single
hexagon does not change the sign sequence sum. As we see in fig. 15.2,
no matter where we leave the hexagon, the sum of the signs within the
flexagon is zero; passing about the center of the flexagon once
or more does not change the sums. A similar demonstration will give the
corresponding result for tetraflexagons: when the plan is placed on a square
lattice, the incoming and outgoing hinges must be parallel and they must
fall on lines separated by an even number of squares:
![]() (see fig. 15.3, in which a plan beginning on a dark line must end on a
dark line).
(see fig. 15.3, in which a plan beginning on a dark line must end on a
dark line).


These examples lead us to ask not what sign sequences, but what plans,
or actual arrays of ![]() gons, can be folded into a flexagon. In this case,
there are
gons, can be folded into a flexagon. In this case,
there are ![]() possible positions for the hinges on either end. Since there
are only
possible positions for the hinges on either end. Since there
are only ![]() different possible values for the sign sequence sum, it will
follow that there are at least
different possible values for the sign sequence sum, it will
follow that there are at least ![]() ways of hinging the ends together that
allow the sign sequence sum to be zero. Thus, for example, any linear
array of triangles except a
ways of hinging the ends together that
allow the sign sequence sum to be zero. Thus, for example, any linear
array of triangles except a ![]() spiral can make at least one
flexagon.
spiral can make at least one
flexagon.
Returning to the problem of ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,...sign sequences,
it may
be pointed out just how the zero degree faces arise. At some point in the
map, two consecutive faces of one cycle will lie on the edge of the map.
Then they will correspond to the signs
,...sign sequences,
it may
be pointed out just how the zero degree faces arise. At some point in the
map, two consecutive faces of one cycle will lie on the edge of the map.
Then they will correspond to the signs ![]() ,
, ![]() , and the
, and the ![]() cut across
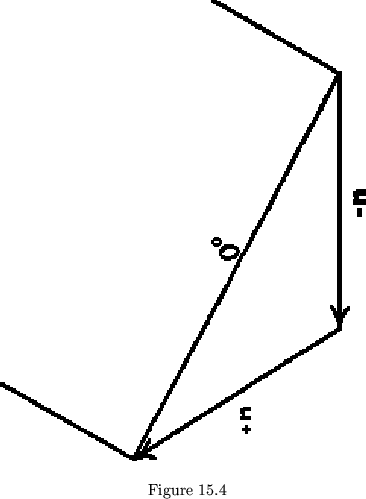
them will have to be a zero-degree face (see fig. 15.4). The leaves which
corresponded to these two signs would have to be folded together, whereupon
the two hinges going to and leaving them would coincide. The only case
where this problem does not arise is in the sequence
cut across
them will have to be a zero-degree face (see fig. 15.4). The leaves which
corresponded to these two signs would have to be folded together, whereupon
the two hinges going to and leaving them would coincide. The only case
where this problem does not arise is in the sequence ![]() ,
, ![]() , the trivial
flexagon.
, the trivial
flexagon.
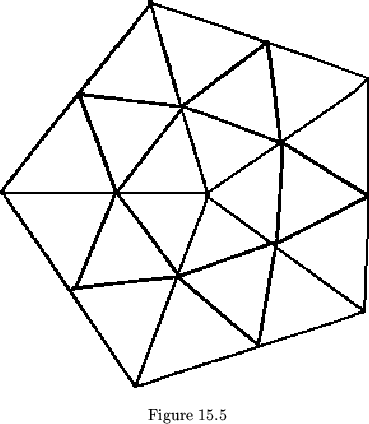
Certain restrictions must be placed on the constant orders that stand for flexagons. Notice, for example, that the permutation 14253 is useless, for it leads to the polygon network and map shown in figure 15.5. Flexing is impossible in this flexagon, because the Tuckerman tree is a closed loop. Impossible constant orders can be described most easily by their polygon networks, in which at least two polygons will be joined along an edge, rather than a vertex only. This in turn happens precisely when a pair of network lines is joined by more than two disjoint routes in the network.