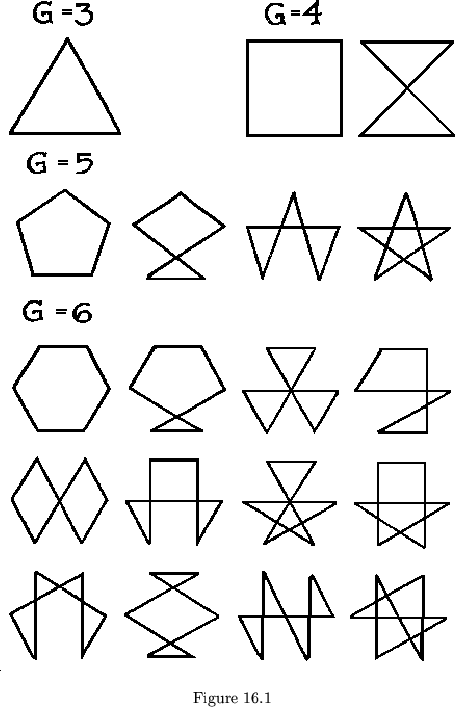By analogy with the problem of counting triflexagons of a given order, we might ask how many G-flexagons there are of order
It might be said that the most interesting mathematical problems concerning flexagons arise when one begins to count them. Certainly Oakley and Wisner's treatment of the triflexagons shows both that these combinatorial problems are non-trivial and that their solutions may throw light on the flexagon problem in general.
However, aside from the results which Oakley and Wisner have
obtained, it appears that little is known in this direction, and the
present authors cannot at this time produce many answers. Still, it
seems worthwhile to at least formulate some of the remaining problems,
in the hope that this will encourage solutions.
By analogy with the problem of counting triflexagons of a given
order, we might ask how many G-flexagons there are of order ![]() . This
question still allows ambiguity: are we to allow incomplete cycles or
not?. If we do, we are essentially counting the total number of different
flexagons of cycle less than or equal to
. This
question still allows ambiguity: are we to allow incomplete cycles or
not?. If we do, we are essentially counting the total number of different
flexagons of cycle less than or equal to ![]() or of mixed cycles less than
or equal to
or of mixed cycles less than
or equal to ![]() . This seems superficially related to the problem of the
total number of flexagons, with mixed or non-mixed cycles, with order
. This seems superficially related to the problem of the
total number of flexagons, with mixed or non-mixed cycles, with order ![]() ;
i.e., the number of dissections of a polygon into polygons by non-crossing
segments joining the vertices. Then again, we might not include incomplete
cycles at all, thus seemingly simplifying the question considerably.
;
i.e., the number of dissections of a polygon into polygons by non-crossing
segments joining the vertices. Then again, we might not include incomplete
cycles at all, thus seemingly simplifying the question considerably.
In any of these cases, we have not considered face degrees at all.
We might ask, for instance, how many different 1-flex cycles one could
have about a single cycle of a G-flexagon, as shown in figure 16.1 for
![]() . Or, if partially tubulating flexagons are not considered, how many
different possible arrangements in all are there per G-cycle?. Then again,
we may decide not to allow zero-faces in each of these cases. All of
these problems are extended by asking how many different G-flexagons can
be made with K-gons, for
. Or, if partially tubulating flexagons are not considered, how many
different possible arrangements in all are there per G-cycle?. Then again,
we may decide not to allow zero-faces in each of these cases. All of
these problems are extended by asking how many different G-flexagons can
be made with K-gons, for ![]() .
.
There is always the problems of counting the flexagons whose maps
possess some special property, such as rotational or mirror-image symmetry
or being made up entirely of some pat structural unit, as with the regular
triflexagons. The number of self-dual flexagons is not known even for
![]() , and no fruitful work at all has been done on the number of flexagons
derivable from a given sign sequence, nor on the number of distinct sign
sequences of a given order.
, and no fruitful work at all has been done on the number of flexagons
derivable from a given sign sequence, nor on the number of distinct sign
sequences of a given order.
There are one or two easier questions whose answers can be supplied
readily, to end on a promising note. The total number of faces in the
G-flexagon
is twice the number of paths. If cut-offs are not included in
the count, there will be
![]() faces; if cut-offs are
included, this
becomes (G+1)(N-2)+2. These figures hold only when applied to complete
flexagons.
faces; if cut-offs are
included, this
becomes (G+1)(N-2)+2. These figures hold only when applied to complete
flexagons.
In order to find the number of map paths touching a given side,
without drawing the map, proceed as for triflexagons, but reducing sequences
of ![]() consecutive numbers instead of mere pairs of consecutive numbers.
In this way a minimum number
consecutive numbers instead of mere pairs of consecutive numbers.
In this way a minimum number ![]() of different leaves are eventually left.
The number of paths touching the given side is then
of different leaves are eventually left.
The number of paths touching the given side is then
![]() ;
note that this is just
;
note that this is just ![]() for
for ![]() and
and ![]() for
for ![]() . If cut-offs are to be counted among the map paths touching
the face, then the number of such paths is simply
. If cut-offs are to be counted among the map paths touching
the face, then the number of such paths is simply ![]() .
.