One direction to extend the flexagons would seem to be to higher dimensions. Though this has not yet been done, the thought led to some study of hinged tetrahedra.
Two tetrahedra may be joined by a long double hinge so as to roll
around one another. The two hinges are arranged so that while one winds
off the first tetrahedron onto the second, the other hinge winds from
second to first tetrahedron. This type of hinging, similar to flexagon
hinging, is exactly like that on swinging doors. The hinge is ordinarily
long enough to wrap around all four faces of the tetrahedron, and has one
end fastened to each tetrahedron (see fig. 17.1). Several different
arrangements of hinges are possible, exhibiting the faces in different
orders, but that shown seems most stable. Its hinge is a ![]() strip
of equilateral triangles, split down the middle.
strip
of equilateral triangles, split down the middle.

A little more interesting but a little bit less related to the flexagons are smokerings, which are rings of polyhedra hinged together end-to-end, each being hinged to the next along one edge. Although many polyhedra may be made to do this, tetrahedra are the only regular polyhedra which will form a ring when joined by diametrically opposite edges to the adjoining tetrahedrons.
The common smokering is a loop of eight regular tetrahedra joined end to end (see fig. 17.2). The number of tetrahedra is generally even, since the opposite edges are perpendicular, and the hinges at the ends of a chain of an odd number of tetrahedra are also perpendicular. Eight is the smallest number of tetrahedra that will both form a ring and exhibit the interesting property of smoke-rings called twirling. In twirling, all of the tetrahedra are simultaneously rotated about an axis passing through the midpoints of the hinged edges. The overall effect of the process is that the smokering as a whole turns inside out. Although there is nothing theoretically complicated about twirling, the effect is fascinating, especially if the smokering is brightly colored.
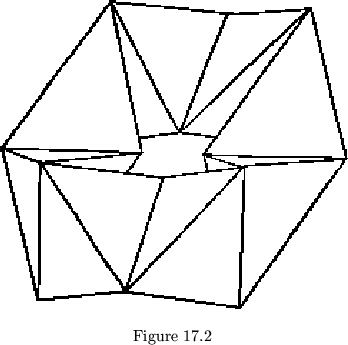
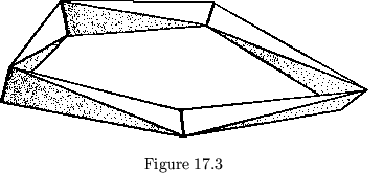
Six tetrahedra may form a ring, but the ring is too tight to twirl. If more than eight tetrahedra are used, the loop becomes looser and looser, until 22 tetrahedra can be tied into a knot. If the tetrahedra are stretched slightly, a ring of an odd number may be formed. If moderately irregular tetrahedra are allowed, a smokering may be made of five tetrahedrons. This ring will twirl one piece at a time, with only two tetrahedra moving at once (see fig. 17.3). Four tetrahedra may form a non-rigid ring, but they will not twirl completely. A smokering of three tetrahedra is rigid.
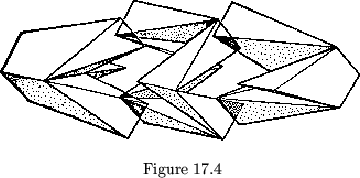
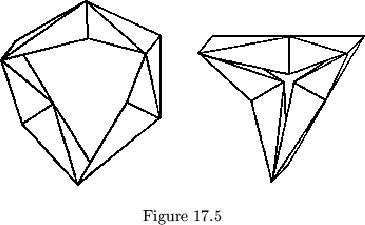
A cube may be dissected into three sections, one of which is a smokering of six irregular tetrahedra. The two remaining pieces are identical (see fig. 17.4). The smokering has two different types of positions, shown in figure 17.5, due to the dissimilarity of the component triangular faces.
Suppose we mutilate a smokering by removing two corresponding sides of each hollow tetrahedron, but so that the ring will still hold together. Then each tetrahedron introduces one quarter-twist into the resulting strip (of paper). There will be one half-twist for every four triangles in the strip. Thus a smokering might conceivably be described as two intertwined flexagons, each of which has the wrong number of twists to actually be a flexagon. One of the very few cases in which a real flexagon will produce a real smokering is that of a mixed flexagon of six units, four of these of order three and the others of order two -- a fairly sad specimen of a flexagon.