Mushrooms are related to smokerings only in that they both can be said to twirl. That is, mushrooms are ring-shaped, and their peculiarity is that they rotate about a looped axis passing through the body of the mushroom. Beyond this, however, the similarity is slight.
Mushrooms are made from two or more strips of polygonal paper leaves. The strips are intertwined so that no flaps result and so that the result is a pile of leaves which holds rigidly together. Mushrooms are not as satisfying as flexagons, in a way, in that their properties rest on the fact that paper is not, after all, rigid, and that if long enough strips are interwound, the mushroom can be bent into a ring and the ends may be joined.
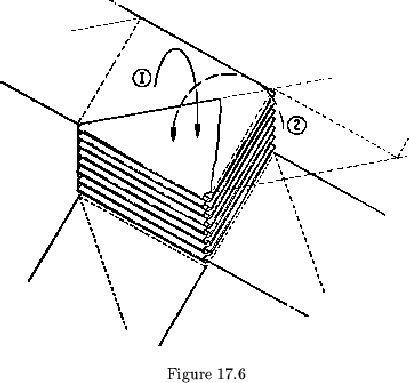
The mushroom that may be made from equilateral triangles is wound
up quite tightly, as shown in fig. 17.6. Two strips are used, both with
the sign sequence ![]() . The finished mushroom, which may require
several hundred leaves, appears in fig. 17.7.
. The finished mushroom, which may require
several hundred leaves, appears in fig. 17.7.

Two straight strips of squares, if folded together like soda straws,
form a much looser mushroom, with four faces. Two or three ![]() square strips may be wound (braided) together to give other four-faced
mushrooms. Similarly, for the higher polygons many different strips
produce corresponding mushrooms, with little significant structural
variation.
square strips may be wound (braided) together to give other four-faced
mushrooms. Similarly, for the higher polygons many different strips
produce corresponding mushrooms, with little significant structural
variation.
Returning to the four-faced mushroom made up of two straight strips of squares, we find that it is not nearly as rigid as was the mushroom made of triangles. The problem presents itself of finding the shortest possible strips of squares for building this mushroom. Surprisingly enough, it turns out that each strip need be only eight squares long. However, such a small mushroom cannot be obtained without several concessions; each square must be creased along both diagonals, there is no longer any hole in the center, the mushroom lies flat, and twirling no longer occurs as a simple continuous operation. In regard to the latter requirement, we recall the equilateral triflexagon of order 3, which resulted from the imposition of similar minimality requirements on a 3-twist Moebius band. It was found necessary to divide the strip up into triangles, the central hole disappeared, the flexagon lay flat, and there was no longer the simplicity and continuity of the process in the Moebius band corresponding to flexing (i.e., rotating the band along its length, about the central hole, while keeping the position of the twists fixed). And just as the flexagon became a new object, the squashed-flat mushrooms are no longer called mushrooms, but bregdoids.
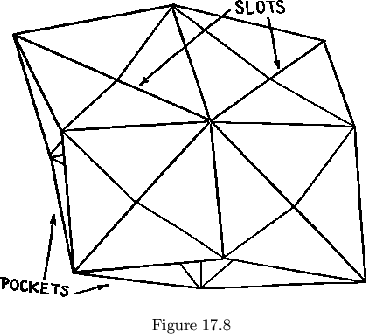
The bregdoid we have just described is shown in fig. 17.8. As in flexagons, we have two surfaces showing, each of which is to be called a side. However, a third set of leaves may also be found, between the two sides, in the pockets (see fig. 17.8). Since the mushrooms formed from squares have four faces, it should hardly seem unnatural for this bregdoid to have four sides. In fact, four positions or faces are possible, depending on how the ends of the strips are joined together. Each of these faces shows two sides, but the sides come in pairs, so that each of two faces will show the same sides. To clarify, if the sides are numbered 1, 2, 3, and 4, two faces will show sides 1 and 3, say, and the other two faces will then exhibit sides 2 and 4. The difference between the two faces showing each pair of sides is the side that may be found in the pockets.
The problem now is to find out how to twirl the bregdoid. From observing twirling in smaller and smaller mushrooms, it becomes clear approximately how it will work for bregdoids. Each face exhibits three sides; the fourth side is hidden, and corresponds to the one side that is usually hidden in a mushroom. Thus twirling commences with hiding a new side; as in flexagons, the lower side is chosen. This is done by widening the pockets downward. From this position we know that we can open out the bottom end of the bregdoid so that it will lie flat; it then stands to reason that if the slots in the upper side (see fig. 17.9) were converted into pockets, and the pockets into slots, that the top end of the bregdoid would open out flat, completing the twirl. This is done either by the crude method of simply pulling apart the slots, forcing them to open into pockets, or by folding the leaves together above the slots first, then opening out the new pockets, which does not force the leaves, and is therefore a little easier on the bregdoid.
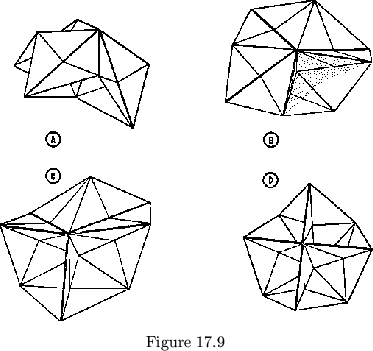
Once we can twirl, it is easy enough to paint all the sides and find the map. As with flexagons, the map for bregdoids made of squares is itself a square. The faces having common sides lie diagonally across from one another.
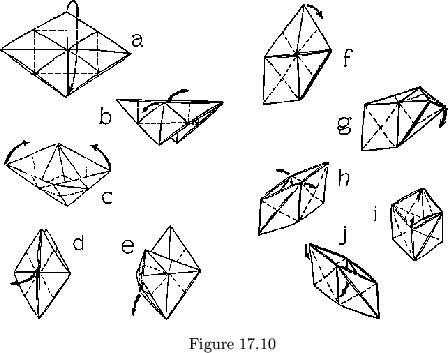
If we tally up the area of the inside of the pockets, we see that it is actually twice the area of one side. Moreover, if the sides are painted, half of each pocket remains white. In fact, just half of the area of the bregdoid ever turns up as a side, unlike the situation for flexagons. When the bregdoid is unwound, it turns out that, in each component square leaf, there are four right triangular sections; one is painted on both sides, the two joining to the adjoining leaves are painted on one side only, and the remaining triangle is blank. There are four different ways of rewinding the two strips so that triangles folded together are colored alike, and the results are quite different. One method, of course, gives back our colored bregdoid. Two others, however, mix the colored and white triangles in various ways, and the fourth makes all the sides blank. These four arrangements exhibit a kind of duality; the colored with the white, and the two mixed ones with each other; each arrangement can be converted to the dual arrangement by a special process due to Peter Hartline (fig. 17-10). In each pair, the two strips are wound in the same direction, only all the hinges are reversed. Since all four positions have the same leaf structure, the maps are the same, and joined together by the dualization process.
Bregdoids can be derived from other mushrooms, and may be made with
more than two strips of paper. A bregdoid has been made from hexagons
which does not lie flat; it stands up, with a thickness of about ![]() its
diameter. No bregdoids have been designed having maps of more than one
cycle, though. In this respect they are less complex than flexagons.
However, there is a case for considering one-cycle flexagons as one-strip
bregdoids, made from
its
diameter. No bregdoids have been designed having maps of more than one
cycle, though. In this respect they are less complex than flexagons.
However, there is a case for considering one-cycle flexagons as one-strip
bregdoids, made from ![]() chains of polygons. From this point
of view, flexing becomes a sort of specialized twirl.
chains of polygons. From this point
of view, flexing becomes a sort of specialized twirl.
Bregdoids, like flexagons, have a basic unit which, in the case of the
square bregdoid studied above, was repeated four times. Needless to say,
any number of repetitions will suffice, if it is greater than ![]() , and
, and ![]() may even be enough for polygons of more sides. Also, bregdoids have been
made from irregular polygons; these may require many units, and do not in
general lie flat at any time.
may even be enough for polygons of more sides. Also, bregdoids have been
made from irregular polygons; these may require many units, and do not in
general lie flat at any time.