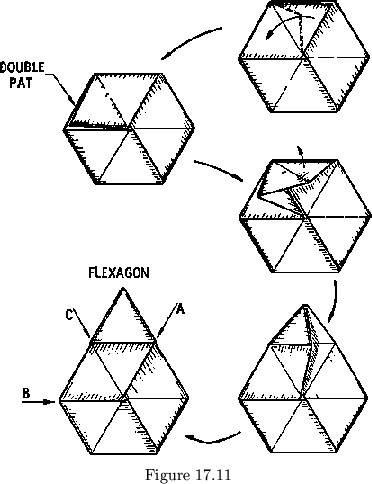
The fleptagons have not been studied very thoroughly, since they are in general both complex and physically unstable. One of the simplest fleptagons is materially identical to a four-unit equilateral triflexagon of order 3. To produce the fleptagon, one unit is partially flexed, as shown in fig. 17.11. The resulting object looks like a flexagon with an extra flap, but it is structurally quite different from the flexagon, and it operates quite differently as well. As the figure suggests, the seven pats are structurally independent, in that there is no symmetry such as that which in the flexagon gives rise to the unit. A fleptagon is operated by folding it over double along any one of the central diagonals marked A, B, and C in figure 17.11. It may then open out, somewhat like a two-unit flexagon, to produce a new fleptagon structure.

The biggest difference between flexagon and fleptagon is that the latter, in "flepping", may not completely change all of the leaf surfaces showing. That is, the "side" has lost any meaning or integrity, when thought of as independent of the faces. Thus a fleptagon map shows only the relation-ships among the faces, or possible states, of the fleptagon. The faces, since they may have common leaf surfaces, cannot be specified in the usual way. Also, there may be many more faces possible in a fleptagon than in a flexagon of corresponding size, since more permutations of the leaves may be allowed. Then again, there may be far fewer faces, depending on the structure of the fleptagon. The number of faces is not uniquely determined by the order of the fleptagon, which is defined as the number of leaves in the plan.
Fleptagon plans are as irregular as the rest of the subject; there need be no repeated unit, as with flexagons. It is not known either how to construct fleptagons, what fleptagons are possible, how many there are, or even along what diagonals they must be folded to flep. Part of the reason why so little has been done in this direction is that even small fleptagons, like flexagons with too many units, tend to disintegrate in various ways.
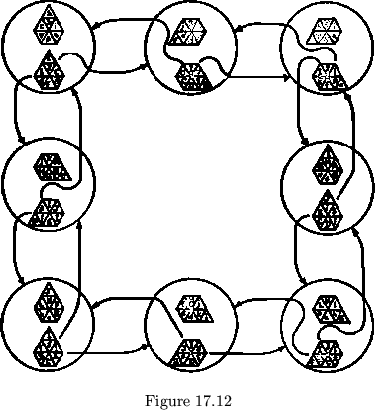
In the fleptagon maps given in fig. 17.12 and 17.13, each face has been diagrammed, front and back, to show the structure clearly. Also, the diagonals used in each flep are shown. Each of these fleptagons shows a characteristic of more complex flexagons; one illustrates a branching map, which is characteristic of change of cycle in flexagon maps; the other map shows that fleptagon maps can have a cyclic structure. No multi-cyclic fleptagons have been built, but these two maps suggest their possibility.
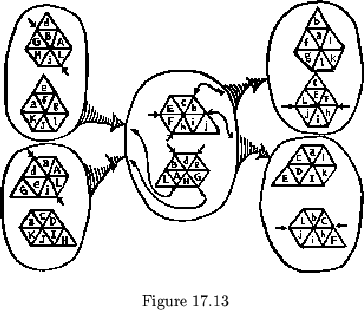
It would be nice if analogues of the various face degrees, cycles, and classes of flexagons could be discovered in the fleptagons, since the theory is at present unknown.