So far little has been said of the internal structure of the pat, although it is the basis of almost every significant feature of the flexagon. To treat the pat structure effectively in discussion or theory, the most important requirement is a workable representation. Basically, two kinds of representations are possible. The first is exemplified by the number sequence, which we have already encountered. In this system, generally, an invariant ordering of the outer map faces is established (in the case of the number sequence, these faces are numbered consecutively about the map rim) and then the corresponding ordering of the leaves in the plan which give rise to the corresponding map rim faces is given (this ordering being in effect the basic number sequence, or number sequence consisting of the lower numbers only from the pairs facing one another across the middle line). In the (basic) number sequence the first ordering system of consecutive numbers about the map rim is fixed, so that it need not be specified for each flexagon. However, we are able to fix this order only to within a constant, so to speak; i.e., the flexagons having number sequences
![]()
(mod ![]() ) are identical in structure. The important thing is, then, that we control our numbering convention of the map rim faces while describing the pat structure in this manner.
But we have already seen the rather complex manner in which such a system fixes the flexagon's pat structure.
) are identical in structure. The important thing is, then, that we control our numbering convention of the map rim faces while describing the pat structure in this manner.
But we have already seen the rather complex manner in which such a system fixes the flexagon's pat structure.
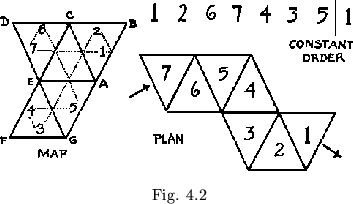
In the other basic system of pat representation the leaves in the plan are given some fixed ordering (usually by numbering them consecutively; this again will be effective only to within a constant) and the resultant map rim ordering is recorded. One system using this method is, for reasons that will be given shortly, called the ``constant order'' numbering system. To give an example of this system, consider first the flexagon shown in figure 4.1. It has the number sequence and plan shown. To use the constant order numbering system, the leaves in the plan are labeled consecutively, the flexagon is folded up, and the corresponding ordering of map rim faces is recorded. The results appear in figure 4.2. Just as the number sequence was essentially a sequence of numbers copied from leaves in the plan, the constant order is a sequence of numbers copied from the map rim, taken consecutively. The constant order is in several respects the inverse or dual of the basic number sequence, as we shall see.
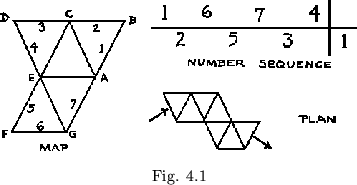
So far, neither of these systems appears to be a representation of the pat structure, on the face of it. However, their relationship to the pat structure becomes apparent when we consider as follows: When a flexagon is assembled, leaf faces that are colored or numbered alike are always placed together facing one another, and from then on, no two differently colored leaf faces are opposed. For, during the ordinary legitimate flexagon o-perations, such different leaf faces are at no time brought together. Even during flexing, when a leaf face is folded away out of view, it is made to do so by placing it face to face with another similarly colored leaf face. Also, each unit contains two leaves colored each color, with two unequal colors appearing on the other sides of these leaves. A little reflection will shown that any two opposed leaves will not only have the same color on the facing sides, but will have distinct colors on the non-facing sides, and thus, since we know uniquely (within any one unit) the only two leaves which can ever possibly adjoin a given leaf in the folded up flexagon, we can completely des-cribe the flexagon's structure. That is, knowing the leaf-to-leaf structure, we can figure out the order of the leaves when the flexagon is assembled. This order, as we saw above, cannot change, whatever ``legal'' operations are performed upon the flexagon; the chain of leaf-to-leaf adjacencies is disrupted only when some particular color must ``come out of hiding'' and be exposed. When this color is again concealed, the constant structure of the leaves is restored.
What, quantitatively speaking, is this constant structure? It is the same as the constant order of the constant order numbering system. To see this, recall that consecutive map rim faces are those having common sides. Thus the two leaves corresponding to adjacent map rim faces will have one color in common and will fall consecutively in the constant structure. It follows that the map rim faces, taken in order about the edge of the map, will fall in the same order as the corresponding leaves, taken in the order in which they lie over one another in the flexagon.
The two numbering systems, each of which is found to be quite useful, are not the only ones, however. The most important variant was developed by C. O. Oakley and R. J. Wisner, who were able to apply it very effectively to the construction or a fruitful analytical flexagon theory.4.1 Their system, which is related to the constant order numbering system, treats the pats singly, rather than dealing with the flexagon as a whole. The map is not used at all in their treatment, the pats alone being analysed in the light of their structure.
A pat is designated by a permutation of the first ![]() integers, where
integers, where ![]() is the number of leaves in the pat, called its ``degree''. The pat is named by first laying out the pat plan from which it was constructed and labeling the leaves along the strip consecutively. Thus the first plan leaf is labeled ``1'', the last ``D''. The pat structure is now obtained from the reassembled pat by reading down through the pat, as though by peeling off single leaves successively. Hence the pat structure may be thought of as a constant order for a single pat, in which the leaf fastened to the ``ingoing'' hinge is always labeled ``1''. The ``ingoing'' and ``outgoing'' hinges are to be carefully distinguished; this seeming artificiality is important when pats are combined to make flexagons. Then the ``ingoing'' hinge of one pat is always the ``outgoing'' hinge of the next. Also, in recording the pat structure for the two pats in a flexagon face, the pat theory convention is to read off the structure from top to bottom for both pats with the same side on top, unlike the constant order method.
is the number of leaves in the pat, called its ``degree''. The pat is named by first laying out the pat plan from which it was constructed and labeling the leaves along the strip consecutively. Thus the first plan leaf is labeled ``1'', the last ``D''. The pat structure is now obtained from the reassembled pat by reading down through the pat, as though by peeling off single leaves successively. Hence the pat structure may be thought of as a constant order for a single pat, in which the leaf fastened to the ``ingoing'' hinge is always labeled ``1''. The ``ingoing'' and ``outgoing'' hinges are to be carefully distinguished; this seeming artificiality is important when pats are combined to make flexagons. Then the ``ingoing'' hinge of one pat is always the ``outgoing'' hinge of the next. Also, in recording the pat structure for the two pats in a flexagon face, the pat theory convention is to read off the structure from top to bottom for both pats with the same side on top, unlike the constant order method.
The pat structure of a flexagon, then, will apparently vary radically under flexing and even turning over. The leaves are renumbered, the pat degrees change, etc. For this reason, the structures of the two unlike pats must be kept separately. The notation used is
![]() , where
the comma separates the two pats, of degrees
, where
the comma separates the two pats, of degrees ![]() and
and ![]() . Thus, for example, the faces indicated in figure 4.3 by half arrows have the pat structures:
. Thus, for example, the faces indicated in figure 4.3 by half arrows have the pat structures:

The pat next to be divided in flexing is always placed to the right of the comma. We can now, in fact, describe what happens during flexing.

Oakley and Wisner's treatment, which we may for convenience call the ``pat theory'', is essentially based upon several simple observations concerning flexagons. The most important of these is the identification of the position of the thumbhole in each pat by structural considerations only, i.e., using the pat structure notation only.
The distinguishing feature of a thumbhole is that all of the leaves either above or below it in the pat are connected only among each other. That is, the part of the pat above the thumbhole is connected to the part below by exactly one hinge. This means that a thumbhole will occur in the pat at precisely those places where all the numbers to the left in the pat structure notation are greater than all of those to the right.
The second observation is that, when two pats are adjoined to produce a larger pat, as in flexing (or in generating a larger flexagon, which we have seen is equivalent to flexing), a new thumbhole is produced, naturally, since the two old pats remain in their old constant orders, but the old thumbhole in each pat is suppressed. Thus if two pats, each with a thumbhole, are combined, the resulting pat still has but a single thumbhole. How can this happen? Suppose, using pat structure notation, our old pats were:
where the only thumbholes are between ![]() and
and ![]() and between
and between
![]() and
and ![]() . Then all of the
. Then all of the
![]() are less than the
are less than the ![]() , and
, and ![]() . Now if we assume that the first pat above will be on top in the new pat, the only arrangement of the new pat that will have only one thumbhole, between the
. Now if we assume that the first pat above will be on top in the new pat, the only arrangement of the new pat that will have only one thumbhole, between the
![]() subpat and the
subpat and the
![]() subpat, and which will maintain the constant orders of both of the old pats, is:
subpat, and which will maintain the constant orders of both of the old pats, is:
This is, in fact, precisely the experimental result when two pats are combined to produce a new one: the two old pats are inverted first, then joined in the correct order.
Notice that leaves are necessarily renamed during the course of the joining, since there are now ![]() more leaves than before in the
more leaves than before in the
![]() pat. In this way advantage in taken of the ambiguity of a constant in the order two systems of pat structure notation. Note also that so long as the two things joined were pats with one thumbhole each, the new thing will clearly be such a pat too. The inverting of subpats before joining them corresponds to the complicated inverting of the number sequence that occurred during primitive flexagon construction in the last section, when it was said that we try to have the new hinges connect leaves which are as distant as possible.
pat. In this way advantage in taken of the ambiguity of a constant in the order two systems of pat structure notation. Note also that so long as the two things joined were pats with one thumbhole each, the new thing will clearly be such a pat too. The inverting of subpats before joining them corresponds to the complicated inverting of the number sequence that occurred during primitive flexagon construction in the last section, when it was said that we try to have the new hinges connect leaves which are as distant as possible.
Now we can see our way clear to another pat theory conclusion: allowing for pats of thickness one ( no thumbholes), all other pats may be built by the above process. This gives us a recursive definition of a pat, and its characterization by a permutation of integers. A pat is either a single thickness or the combination of lesser inverted pats.
Using this algorithm it is easy enough to construct all possible pats of low degrees, as in Table 4.1. Notice that the pat of degree ![]() is by no means unique. There are in fact
is by no means unique. There are in fact
![]() pats of degree
pats of degree ![]() , as Oakley and Wisner demonstrate.
, as Oakley and Wisner demonstrate.
| Degree | Pat | Degrees of |
| of Pat | Structure | Component |
| Subpats | ||
| 1 | 1 | - - |
| 2 | 2,1 | 1 1 |
| 3 | 23,1 | 2 1 |
| 3 | 3,12 | 1 2 |
| 4 | 324,1 | 3 1 |
| 4 | 243,1 | 3 1 |
| 4 | 34,12 | 2 2 |
| 4 | 4,213 | 1 3 |
| 4 | 4,132 | 1 3 |
| 5 | 2534,1 | 4 1 |
| 5 | 2453,1 | 4 1 |
| 5 | 3254,1 | 4 1 |
| 5 | 4235,1 | 4 1 |
| 5 | 3425,1 | 4 1 |
| 5 | 435,12 | 3 2 |
| 5 | 354,12 | 3 2 |
| 5 | 45,213 | 2 3 |
| 5 | 45,132 | 2 3 |
| 5 | 5,1423 | 1 4 |
| 5 | 5,1342 | 1 4 |
| 5 | 5,2143 | 1 4 |
| 5 | 5,3124 | 1 4 |
| 5 | 5,2314 | 1 4 |
To get a clearer idea of the possible pat structures, we could consider a pat large and complex enough that none of the subpats or subsubpats or subsub...subpats are of a single thickness. In such a pat the only important feature of pat construction is that each pat is composed of two inverted subpats. Then the situation may be diagrammed using a permutation graph (see figure 14.2). The vertical axis may be thought of as height of the subsub...subpats above the bottom of the pat, the horizontal axis as distance of each subsub...subpat from the ingoing hinge. This kind of pat, in which doubling is uniform throughout the subpat structure, will be found in star flexagons. Other flexagons may have single leaves where the graph shows subpats, thus suggesting the idea that all flexagons arise from star flexagons by various deletion processes.
But if we accept the above definition of a pat, what is a flexagon? Pat theory's concise and obvious answer is that a flexagon is an ordered pair of pats. The two pats are ordered so that it will be meaningful to rotate the flexagon. Precisely, rotation interchanges the two pats. Since we can find thumbholes, flexing can be concisely defined as a specific manipulation of the integers comprising an ordered pair of pat-structure-notation pats: flexing carries flexagons of the form
![]() into the flexagons
into the flexagons
![]() ,
when there is a thumbhole between
,
when there is a thumbhole between ![]() and
and ![]() . Note that the last (lowest) part of the second pat becomes the new first (highest) part of the first pat. The other subpats are merely inverted.
. Note that the last (lowest) part of the second pat becomes the new first (highest) part of the first pat. The other subpats are merely inverted.
The trouble with the pat theory's definition of a flexagon from our point of view is that when we perform one of the legitimate flexagon operations we get a completely new and not obviously related ordered pair of different pats. Thus the physical flexagon really corresponds to an equivalence class of ![]() pat theory flexagons, where
pat theory flexagons, where ![]() is as always the order of the flexagon(s), or, equivalently, the sum of the degrees of the two pats.
is as always the order of the flexagon(s), or, equivalently, the sum of the degrees of the two pats.
However inconvenient this may appear in terms of building and operating specific physical flexagons, this system clearly reduces the flexagons to a set of permutations with seemingly workable constraints. Hence the pat theory provides a valuable tool in calculating the number of flexagons possible for a given order. The only real complication is that the ![]() pat structures per flexagon are not necessarily distinct; in fact, we can see just when duplications of a single pat structure will occur by examining the symmetry of the map. Thus the flexagon shown in figure 4.4a will have 10 rather that the expected
pat structures per flexagon are not necessarily distinct; in fact, we can see just when duplications of a single pat structure will occur by examining the symmetry of the map. Thus the flexagon shown in figure 4.4a will have 10 rather that the expected ![]() distinct pat structures, that in figure 4.4b
distinct pat structures, that in figure 4.4b ![]() instead of
instead of ![]() . These duplications must be counted out of the final tally. Fortunately, the two symmetries shown are the only ones, and they always occur separately, never together in the same flexagon.
. These duplications must be counted out of the final tally. Fortunately, the two symmetries shown are the only ones, and they always occur separately, never together in the same flexagon.
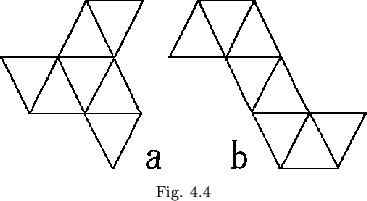
One final difference between the pat theory flexagon and the ordinary physical flexagon involves the direction of winding up a flexagon. An ordinary paper flexagon may be wound up in two directions, depending upon which way the first fold is made, or, alternatively, if this has been determined already by the flexagons coloration, which direction of turning in the Tukey triangle network (in finding the sign sequence) is assigned a + value. These two ways do give slightly different flexagons, one being the mirror image of the other. Ordinarily this distinction is neglected or, if a convention has been established, corresponds to making a mirror image of the map. Often, even then, symmetry of the map may make these two mirror image flexagons identical, as with that shown in figure 4.4b. However, the pat theory naturally detects this distinction and, in counting the number of possible flexagons, will include both right- and left-handed versions. These may be accounted for later, in which case the usual figures for the number of possible flexagons are finally obtained.
To further illustrate the power of the pat theory, Oakley and Wisner calculate the number of possible regular flexagons in a similar fashion. They must here add the restriction that the sum of the degrees of the two pats be a multiple of three, but with neither of the degrees themselves ever a multiple of three. It is then necessary for one pat to have degree ![]() , the other
, the other ![]() , where
, where ![]() and
and ![]() are any integers.
The fact that regular pats may not be order divisible by three may be seen empirically; the reason should become clear later 4.2 . Again we are able to formulate a simple recursive definition of the (regular) pat, with
are any integers.
The fact that regular pats may not be order divisible by three may be seen empirically; the reason should become clear later 4.2 . Again we are able to formulate a simple recursive definition of the (regular) pat, with ![]() -type pats always arising from the adjunction of two
-type pats always arising from the adjunction of two ![]() -type pats, and viceversa, except for the pat of degree one.
-type pats, and viceversa, except for the pat of degree one.
These recursive pat construction techniques do provide a fascinating (if not terribly informative ) method of actually building flexagons. As for the actual calculations for finding numbers of flexagons, they are too involved to appear here. Suffice it to say that, using the various recursive definitions, a number of generating functions are defined and their relations solved to give preliminary results for the number of possible pats of given degree. The number of flexagons of order ![]() then follows, this being refined until the various symmetries are eliminated. The same process is applied to the regular-flexagon problem.
then follows, this being refined until the various symmetries are eliminated. The same process is applied to the regular-flexagon problem.
The resulting values are unwieldily as stated in formulas,
with several different cases. The total number of flexagons
rises roughly as an exponential of ![]() ; a fairly good approximation,
to within about 10% from
; a fairly good approximation,
to within about 10% from ![]() through N=15, is the
expression
through N=15, is the
expression ![]() . The number of regular flexagons rises
roughly as an exponential of
. The number of regular flexagons rises
roughly as an exponential of
![]() except, of course,
that all regular flexagons are of orders divisible by three.
A rough approximation for regular flexagons is given by the
expression
except, of course,
that all regular flexagons are of orders divisible by three.
A rough approximation for regular flexagons is given by the
expression
![]() , for orders less than
, for orders less than ![]() . The actual
values are given in table 4.2 for flexagons of order less than
. The actual
values are given in table 4.2 for flexagons of order less than
![]() . Also included in the table for comparison are values of
. Also included in the table for comparison are values of
![]() , the number of pats of degree
, the number of pats of degree ![]() .
This value is in fact closely related to the value for the number of flexagons, being somewhat less than
.
This value is in fact closely related to the value for the number of flexagons, being somewhat less than ![]() times the number of flexagons of order
times the number of flexagons of order ![]() .
The figure
.
The figure ![]() also occurs in the ratio
also occurs in the ratio
![]() between successive terms in this sequence. The terms in this sequence also arise as the righthand-most terms in the interesting triangle:
between successive terms in this sequence. The terms in this sequence also arise as the righthand-most terms in the interesting triangle:
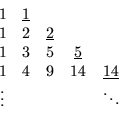
in which each term is the sum of the numbers above it and to its left. The number of regular pats is also included in table 4.2, and the regular pats of degree ![]() are shown.
are shown.
| Number of Flexa- | Number of Pats | Number of | Regular | |
| N=D | gons of Order N | of Degree D | Flexagons | Pats |
| 1 | 1 | 1 | ||
| 2 | 1 | 1 | 1 | |
| 3 | 1 | 2 | 1 | |
| 4 | 1 | 5 | 1 | |
| 5 | 1 | 14 | 2 | |
| 6 | 3 | 42 | 1 | |
| 7 | 4 | 132 | 4 | |
| 8 | 12 | 429 | 9 | |
| 9 | 27 | 1,430 | 1 | |
| 10 | 82 | 4,862 | 22 | |
| 11 | 228 | 16,796 | 52 | |
| 12 | 733 | 58,786 | 4 | |
| 13 | 2,282 | 208,012 | 140 | |
| 14 | 7,528 | 742,900 | 340 | |
| 15 | 24,834 | 2,674,440 | 14 | |
| 16 | 83,898 | 9,694,845 | 969 | |
| 17 | 285,357 | 35,357,670 | 2394 | |
| 18 | 983,244 | 129,644,790 | 74 |
Note: the number of flexagons given here is the reduced value for the number of models mentioned in Remark C, p. 154, of the Oakley-Wisner article. The expression for odd N, corresponding to that given in Remark C for even ![]() , is
, is
![]() .
.
I have also established that the corresponding results for regular flexagons are the reduced values ![]() :
:
![]() , and
, and
![]() .
.
Regular Pats of Degree ![]() :
:
1 2,1 34,12 5,2143 3254,1 67,34125 67,14523 36745,12 56347,12
Returning our attention to the order two flexagon representations, we observe that although the number sequence is equal in value with the cons-tant order in counting the number of flexagons (see the portion of chapter XIV on Duals), when it comes to operating the flexagon using some algorithm like that given for the pat theory, the number sequence is perhaps) less easily interpreted than the constant order, which bears a strong resemblance to the pat theory notation. This is not, however, to say that a suitable algorithm for flexing the number sequence cannot be devised; it would in fact be very similar to that for the constant order. At any rate it should be convenient to know how to convert easily from a constant order to the number sequence of the same flexagon or viceversa.
It will be remembered that the existence of the constant order was demonstrated using the fact that like-numbered leaves always meet in the folded-up flexagon. Hence we may number the ``leaves'' in the number sequence from 1 to ![]() and see which pairs of leaves lie together.
For example, in the sequence
and see which pairs of leaves lie together.
For example, in the sequence
| 1 | 5 | 5 | 4 | 7 | 1 | 6 | 3 | 1 | ||
| 2 | 4 | 6 | 3 | 8 | 8 | 7 | 2 | 2 | , | |
| #: | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 1 |
We way now feel free to discuss the effects of the various operations upon the constant order. First we establish the notion of a face in constant order notation. The constant order may be considered as something like a pat structure for the whole folded-together unit. Then when the flexagon is opened out at a face, to read the constant order we are forced to read through one of the pats upside down. We can uniquely specify any position of the flexagon and at the same time give its structure by indicating how the constant order is split into pats and further indicating which of the two pats is to be read upside down or considered inverted. The latter tells us which surface of the flexagon is up; it corresponds to the pat theory convention of writing all pats from top to bottom rather than bottom to top. The inverted pat is identified by underlining it; the two pats are separated by a comma. Furthermore, the right-hand pat will be the one in position to be split in the next flexing, just as with the pat theory notation. Again using the faces shown in figure 4.3 to illustrate, we have:
| a. | (3, 21) | Constant order: | 132 |
| b. | (43, 521) | Constant order: | 14352 |
| c. | (126, 435) | Constant order: | 126435 |
The initial choice of an underlined pat is arbitrary for each flexagon, and the constant order may vary by a constant or a multiple of ![]() , modulo
, modulo ![]() , so that the same pat structure may have many equivalent representations (more accurately, each flexagon may have many different representations). Face b. above, for example, is identical in structure with any of the follo-wing:
, so that the same pat structure may have many equivalent representations (more accurately, each flexagon may have many different representations). Face b. above, for example, is identical in structure with any of the follo-wing:
![]() , etc.
Once one of these equivalent representations has been chosen for the face at hand, an algorithm for flexing it can be established. This algorithm should preserve the constant order (which is not preserved under the equivalences above, except where the map is symmetrical). It will split the right-hand pat at the thumbhole, which may be located by finding the unique place in the pat where all but two leaves to the right or left (at most) are fastened to each other only. That is, a pat or subpat will always consist of at permutation of consecutive integers, modulo
, etc.
Once one of these equivalent representations has been chosen for the face at hand, an algorithm for flexing it can be established. This algorithm should preserve the constant order (which is not preserved under the equivalences above, except where the map is symmetrical). It will split the right-hand pat at the thumbhole, which may be located by finding the unique place in the pat where all but two leaves to the right or left (at most) are fastened to each other only. That is, a pat or subpat will always consist of at permutation of consecutive integers, modulo ![]() . For Example, in the flexagon face
(3, 4125) the thumbhole occurs between leaves
. For Example, in the flexagon face
(3, 4125) the thumbhole occurs between leaves
![]() and
and ![]() , since 125 is a permutation of consecutive integers
(mod 5). The ordinary constant order may be split into two pats by dividing it so that both pieces satisfy this criterion. Finally, in flexing the whole flexagon is inverted; if we read initially up through one pat and down through the order, after flexing we read down through the first and up through the second. That is, to keep the correct leaves on ``top'' of the flexagon, the ``inverted'' pat must become uninverted and viceversa. The reason for this is that in flexing, the two subpats that remain in their old pats (one of which is, in fact, the old left pat) are actually turned
over, whereas the remaining right subpat changes pats with out being inverted.
, since 125 is a permutation of consecutive integers
(mod 5). The ordinary constant order may be split into two pats by dividing it so that both pieces satisfy this criterion. Finally, in flexing the whole flexagon is inverted; if we read initially up through one pat and down through the order, after flexing we read down through the first and up through the second. That is, to keep the correct leaves on ``top'' of the flexagon, the ``inverted'' pat must become uninverted and viceversa. The reason for this is that in flexing, the two subpats that remain in their old pats (one of which is, in fact, the old left pat) are actually turned
over, whereas the remaining right subpat changes pats with out being inverted.
Within these limitations, there are still two cases that arise, depending upon which pat is underlined: flexing takes the flexagon
![]() into
into
![]() but takes the flexagon
but takes the flexagon
![]() into
into
![]() ,
where the thumbhole lies between
,
where the thumbhole lies between ![]() and
and ![]() . Each of these agrees with the pat theory algorithm; they differ so that turning the flexagon over (which carries
. Each of these agrees with the pat theory algorithm; they differ so that turning the flexagon over (which carries
![]() into
into
![]() and viceversa), flexing it, then turning it back over will not be equivalent to a simple flex. This result should be expected; in fact, this complex operation precisely nullifies the result of rotating, flexing, and rotating once more. This may be checked using the operations defined above. Rotating, of course, carries the flexagon
and viceversa), flexing it, then turning it back over will not be equivalent to a simple flex. This result should be expected; in fact, this complex operation precisely nullifies the result of rotating, flexing, and rotating once more. This may be checked using the operations defined above. Rotating, of course, carries the flexagon
![]() into
into
![]() , and vice versa.
, and vice versa.
This gives us all the information necessary to operate a flexagon in either pat theoretic or constant order notation alone. To execute the Tuckerman traverse, for example, we would proceed as illustrated below for the flexagon shown in figures 4.1 and 4.2:
| Face and | Pat Theory | Constant Order |
| Operation | Notation | Notation |
| A-B Flex | ( 1 , 4 2 3 6 5 1 ) | ( 1 , 2 6 7 4 3 5 ) |
| C-A Flex | ( 2 1 , 4 5 2 1 3 ) | ( 1 2 , 6 7 4 3 5 ) |
| E-C Flex | ( 4 3 5 1 2 , 2 1 ) | ( 4 3 5 1 2 , 6 7 ) |
| D-E Rotate | ( 6 2 1 5 3 4 , 1 ) | ( 4 3 5 1 2 6 , 7 ) |
| D-E Flex | ( 1 , 6 2 1 5 3 4 ) | ( 7 , 4 3 5 1 2 6 ) |
| C-D Rotate | ( 3 2 6 4 5 1 , 1 ) | ( 7 4 3 5 1 2 , 6 ) |
| C-D Flex | ( 1 , 3 2 6 4 5 1 ) | ( 6 , 7 4 3 5 1 2 ) |
| E-C Flex | ( 2 1 , 4 3 5 1 2 ) | ( 6 7 , 4 3 5 1 2 ) |
| A-E Flex | ( 3 4 1 2 , 3 1 2 ) | ( 1 2 6 7 , 4 3 5 ) |
| G-A Rotate | ( 5 6 2 1 4 3 , 1 ) | ( 1 2 6 7 4 3 , 5 ) |
| G-A Flex | ( 1 , 5 6 2 1 4 3 ) | ( 5 , 1 2 6 7 4 3 ) |
| E-G Flex | ( 3 2 5 4 1 , 2 1 ) | ( 5 1 2 5 7 , 4 3 ) |
| F-E Rotate | ( 6 1 4 5 2 3 , 1 ) | ( 3 5 1 2 6 7 , 4 ) |
| F-E Flex | ( 1 , 6 1 4 5 2 3 ) | ( 4 , 3 5 1 2 6 7 ) |
| G-F Rotate | ( 2 5 6 3 4 1 , 1 ) | ( 5 1 2 6 7 4 , 3 ) |
| G-F Flex | ( 1 , 2 5 6 3 4 1 ) | ( 3 , 5 1 2 6 7 4 ) |
| E-G Flex | ( 2 1 , 3 2 5 4 1 ) | ( 4 3 , 5 1 2 6 7 ) |
| A-E Flex | ( 3 1 2 , 3 4 1 2 ) | ( 4 3 5 , 1 2 6 7 ) |
| C-A Flex | ( 4 5 2 1 3 , 2 1 ) | ( 6 7 4 3 5 , 1 2 ) |
| B-C Rotate | ( 6 3 1 2 5 4 , 1 ) | ( 6 7 4 3 5 1 , 2 ) |
| B-C Flex | ( 1 , 6 3 1 2 5 4 ) | ( 2 , 6 7 4 3 5 1 ) |
| A-B Rotate | ( 4 2 3 6 5 1 , 1 ) | ( 2 6 7 4 3 5 , 1 ) |
Notice that the sides associated with each face are easily found from the constant order notation; the top side is that associated with both top leaves, the bottom side is associated with both bottom leaves. The pat structure is derived from the constant order by inverting underlined pats and adding a constant where necessary. To remember the constant order flexing algorithm, we need only keep in mind that it is always the lower right subpat that changes pats. Also, note that in the Tuckerman traverse the single leaves that occur as pats in the constant order notation always appear in consecutive (or as above, inverted consecutive) order.
It is quite difficult, given two pat structures, to find whether they belong to the same flexagon. However, with the constant orders given, the ambiguity of a constant that may arise is easily taken care of by compa-ring the sequences of ![]() terms found by calculating the differences between adjacent terms of the constant orders. There are two ways of taking these differences for each of the constant orders. If the sequences for the two constant orders, which must be considered cyclic, are equal, the flexagons are the same. On the other hand, to calculate whether two constant order faces have the same structure, the simplest thing is to convert to pat theory notation.
terms found by calculating the differences between adjacent terms of the constant orders. There are two ways of taking these differences for each of the constant orders. If the sequences for the two constant orders, which must be considered cyclic, are equal, the flexagons are the same. On the other hand, to calculate whether two constant order faces have the same structure, the simplest thing is to convert to pat theory notation.
Most of the developments of this chapter will be generalized quite easily to cover all of the new flexagons that we will encounter.