- ... theory.4.1
-
C. O. Oakley and R. J. Wisner, FLEXAGONS. American Mathematical Monthly, Vol. LXIV, No 3, March 1957, Pp. 143-154.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... later4.2
- Incoming and outgoing hinges of the pat will overlap, so that a complete pat is not formed, yet further winding is frustrated
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
flexagons 6.1
- However, Dr. F. G. Mannsell and
Miss Joan Crampin (see bibliography) considered flaps,
and presently (sect _____) we will study flexagons
having superimposed hinges.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cycle 6.2
- A
cycle is defined as a series of flexes from a given side back to
that side without retracing any path or turning the flexagon over.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 0 6.3
- From
now on we will consider only the top unit when discussing which
pat the flexagon peels from in flexing. Thus one hinged in the order
1 2 3 0 is called a left-flexing flexagon, while one hinged in the
order 3 2 1 0 is a right-flexing flexagon
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
leaf 6.4
- An
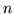 -hinge is one which occupies position
-hinge is one which occupies position 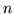 when a unit is folded
together in such a way that the zero hinge connects the two units
of the flexagon.
when a unit is folded
together in such a way that the zero hinge connects the two units
of the flexagon.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 6.5
- This
tubulation, if cut and turned inside out, would produce a
four-cycle. In general, if the effective hinge of a tubulation
is
 , the cycle attempted is
, the cycle attempted is 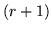 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
sides. 7.1
- Such a leaf is said to be of ``class G'',
as is the corresponding flexagon.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... ``cuts'' 9.1
- A ``cut'' is a shortcut flex which omits one or
more sides. It is a classified
by degree, representing the number of sides they cut out. A
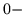 cut is a
flex along the outside of the map polygon. In a proper flexagon, the
cut is a
flex along the outside of the map polygon. In a proper flexagon, the
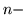 cut is always an
cut is always an 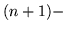 flex.
flex.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... cycle 9.2
- A
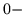 cut cycle ia one composed completely of
cut cycle ia one composed completely of
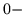 cuts, no matter what the value of flexes involved. Thus, on the map
it is equivalent to following along the outside edge of the map polygon.
cuts, no matter what the value of flexes involved. Thus, on the map
it is equivalent to following along the outside edge of the map polygon.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... flexing 10.1
- The notation ``
 face''
is used to indicate a face of degree
face''
is used to indicate a face of degree 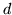 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... show 10.2
- ``
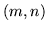 '' refers to the face showing side
'' refers to the face showing side
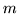 on top and side
on top and side 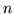 below.
below.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- .... 10.3
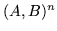 is the
face
is the
face  having face degree
having face degree 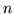 .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Joseph11.1
- See bibliography
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... Wheeler 12.1
- See bibliography
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ...
followings: 13.1
-
 is the face degree and
is the face degree and  the sign sequence
sum for the pat
the sign sequence
sum for the pat 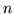 ;
;  is the flexagon's total sign sequence sum.
is the flexagon's total sign sequence sum.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
- ... 14.7) 14.1
- In fact, all regular flexagons are self-dual.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.