 |
Harold V. McIntosh
August 12, 2000
What they are about, is long strips of paper that you can fold up and glue the ends. Once that is done, they can be folded up and unfolded in new arrangements, which is especially evident if you paint the faces, or even more spectacularly, draw pictures.
They were first discovered by some students in Princeton in the late thirties, and got spread around the country because the father of one of them worked at the National Bureau of Standards, where the winners in the Westinghouse Science Talent Search used to be entertained. In fact I am not so sure I didn't hear about them when I was at Brighton High School, because there was some mention of some funny paper strips you could fold.
It was never more than a remark I heard, there wasn't any way of following it up, or much incentive to do so. Of course, in grade school, there were things called ``cootie catchers'' which are a sort or origami and similar, but not the same. Also, one of the kids in BHS had a paper route and a way of folding up the Rocky Mountain News (tabloid, in contrast to the Denver Post) which made great paper airplanes. It was SO close to being a flexagon, but it never occurred to anybody to give it an extra twist to make it a moebius strip. In fact, we were sort of conditioned against moebius strips for their handedness which was felt to violate decent symmetry.
Well, that is prehistory. While I was at Cornell one of the girls in our class had been to the Science Talent Search and one day tried to remember how the things were made. One thing led to another, somebody helped her out by applying the moebius twist with the remark that you had to have symmetry, and after that several people spent time folding up strips of paper; but we never got to the levels the people at Princeton reached. We didn't even know about that part.
Anyway that was my first actual experience with a flexagon, and it didn't take long to figure out some of the simpler attributes, such as the fact that you could double up quite long strips of paper several times and get really fat flexagons. One or two of my friends got interested, and we got as far as making a map of the sequence in which the numbered faces could turn up, and noticing that they turned up in different ways, with different distributions of paper thickenss. No doubt a fair amount of time which should have been spent studying got wasted that way. There was always a suspicion that there should be something written up in the literature, what with there being books on topology, mathematical recreations, and such. What is Mathematics? by Courant and Robbins [1], for example. But the most that ever turned up was a lot of hearsay which never led to anything. For example, one professor thought there was a journal article. In retrospect, he may have been a student at Princeton when the things were being explored there, and may have heard about them. But the only place to look were the math and physics libraries; we never looked very hard, and nothing ever showed up.
Time passed; I wrote up some ideas about mapping a few traditional problems, such as the Towers of Hanoi and the Chinese Ring Puzzle, and included some ideas about a ``covering space'' to generate the maps of the complex flexagons from the simpler ones. Even so, the idea that flexagons could be made out of squares instead of triangles, or that you didn't have to split every face and so could get numerous partial flexagons, never arose.
 |
Flexagons were always something to play with, and one kept one hearing them mentioned, or finding them recognized in one way or another. The next advance was related to the American Mathematical Monthly article [8] published by C. O. Oakley and R. J. Wisner, two professors at Haverford University in Pennsylvania. Another girl of my acquaintance from Cornell had known Oakley's son during High School, so through that contact an appointment was arranged to meet the father. My main recollection of the interview was his viewpoint that flexagons were a theory of blocked hinges - of the double-acting type which are traditional on barroom doors. He and Wisner were also interested in counting flexagons, which is not entirely straightforward when coincidences due to symmetry classes have to be sorted out
Needless to say, we studied their article carefully, since it contained far more detail than a simple description of how to wind up a flexagon. For example, it defined thumbhole and pat and took up the properties of the permutation generated by comparing the sequential position of a triangle along its strip to its position in the vertical stack remaining after the flexagon is all folded up.
Their contribution, which appeared about three months after Martin Gardner's article in Scientific American [5], reflected work of previous months or years, considering the time lag between journal submission, acceptance, and publication, none of which even begins until the article is finally finished. Evidently the same lags should be figured into the Scientific American schedule as well.
Of course, once flexagons were announced in such a widely read popular journal, correspondingly many more people took up an interest in the scheme which would appear to have spread previously mostly by word of mouth from the Westinghouse event.
By that time I was working at Aberdeen Proving Ground, where my supervisor was a very erudite person, chess master, devotee of mathematical recreations, unbearable Turkish cigarettes, and generally, quite an accomplished mathematician. Although he had one or two of the classic books (whose titles I have forgotten), and they dealt with magic squares, knight's tours, and the like, there was nothing resembling flexagons. But the IBM cards used to feed the ORDVAC were an ideal medium for flexagon construction.
Figure 1 shows how the kitchen table got converted into a workshop in those days. Model airplane dope was good for painting the faces of the flexagons; the spots which oozed through the holes were taken to give the combinatiuon an exotic look. Tempera water color paints were also handy. At the time I was also making a plaster cast of a spherical harmonic for the mathematical analysis we were attempting at the proving ground, trying to visualize multipoles, sketch Brillouin diagrams, and in general a variety of artistic tinkering.
Well, there is more of a story, but the summary is that a family I met in Maryland while working at the proving ground had a son looking for a Talent Search project (we were still on the eve of Sputnik, the New Math, and Science Fairs), and although I couldn't think of any ideas, I did show him some toys which I had been working on, one of which was the flexagon. Eventually he decided to work on that - it even got him an honorable mention and admission to Harvard - and over the course of several summers with several persons' participation, we ended up with a huge RIAS report [20] (RIAS, a subsidiary of the Martin Company, is the place I worked after having spent two years at Aberdeen Proving Ground). The whole episode stretched over two or three years or a little more, and accounts for the bulk of the flexagon work which I was actually involved.
It is something of a challenge, sorting out the actual sequence of events after forty years. Martin Gardner's article, although it was a mere description of what a flexagon was and how to fold one up, suddenly gave the whole subject the legitemacy which it had lacked previously, as well as making its contributions to setting the origins straight. It is still a source of wonderment, that flexagons were never part of the origami tradition, something which has a venerable history.
But Gardner's article didn't appear until we were already at work; so much so that, unaware of the extent of his access to the historical roots, we worked up a report [19] with the hope that Scientific American might be interested in a more detailed exposition. Gardner sent it back, with the apology that what had already been published had probably saturated the market. Considering the magazine's need for a continuing supply of novel and not overly detailed material, the reaction was understandable.
Although the meeting with Oakley resulted from personal contacts, it is hard to remember whether he presented us with a reprint or preprint of that article or if I had seen it previously; I do have a reprint in my files. Whatever the timing, this was where we probably got the additional references which they cited and set about tracking them down; and where we first encountered such rigorous definitions as the pat structure, the idea of a pair of permutations, and the transformation of the edge-dual map into the recipe for preparing the labelled strip in advance.
On the other hand, the realization that flexagons could be constructed from squares resulted from one of those nice misunderstandings where a letter describing the flexagon project on the part of one boy was misread by his friend only to reveal an entirely new structure when they finally compared their results!
Another discovery, the bregdoid, was the result of pushing a known structure to its limits. Most people have probably doubled a pair of soda straws back and forth to get an accordion-folded braid at one time or another, and some may have even joined ends to make a bracelet. The true inspiration lay in getting the smallest combination which would lie flat, surely a consequence of the person's family's artistic inclinations and experience.
 |
An element of timing which can be checked, is Martin Gardner's reference to the Oakley-Wisner article, although it is still necessary to factor publication delays into disentangling the relationships among that particular set of authors. In any event, Gardner was an avid collector of recreational mathematics and other bibliographic material, so he doubtless already knew of the articles in Mathematical Gazette, Mathematics Magazine, and so on. But those earlier articles were purely descriptive; such theory as there was lay in reference [8], and presumably in the legendary residue of that Princeton Flexagon Committee.
A third revelation, taken up by Anthony Conrad in [20], consisted in the realization that just about anything could be folded up into a flexagon, if the definitions were accepted liberally,
Martin Gardner actually did a follow-up on his flexagon paper a couple of years later by publishing a description of the tetraflexagon [9]; In the meantime some further personal family contacts had obtained an interview for the boys with John Tukey in his Princeton home. As I recall, written material was still lacking, as well as suggestions for further references, although there was some fairly detailled discussion of tetraflexagons, and tubulation in particular. Why is it that people don't keep a diary, and write down details of interesting meetings so as to be able to refer to them later on?
Those years at RIAS saw some fairly intensive efforts. Younger brothers, casual acquaintainces, and even some of the RIAS summer people got interested. Getting a report finished up wasn't the easiest thing, although we were able to enlist the help of Martin Baltimore's art department and drafting staff. Writing the report is nowhere as much fun as playing with the basic ideas, something which all scientific investigators, writers, and reporters know quite well.
Different people have had different ideas of what makes flexagons work, and even then their ideas seem to have changed from time to time. For example, when we got interested in them at Cornell, one of the obvious things to do was to make a map of the different configurations, which were identified simply by wrting numbers on the triangles in the visible faces. In making the map we distinguished adjacent face thicknesses which made for considerable complication, but soon decided to leave the differences as an implicit understanding and simplify the diagram. Of course, it was a tripartite Cayley tree, and the grouping of different genotypes under one phenotype (as someone expressed a similar situation many years later) may or may not have resulted in a real simplification.
We knew that it was possible to make different thicknesses of flexagons, by folding up longer and longer strips, and at that time I was interested in covering spaces, of the kind which are Riemann surfaces in complex variable theory. So a theory was elaborated for slicing the strip of paper so as to separate the top face from the bottom face whenever a combinatioon turned up where the flexagon could not be opened. But it was never noticed to what extent the process was selective and that the faces need not be peeled apart along the whole length of the strip. Anyway a fair amount of time got wasted, flexing and mapping flexagons, rather than doing homework.
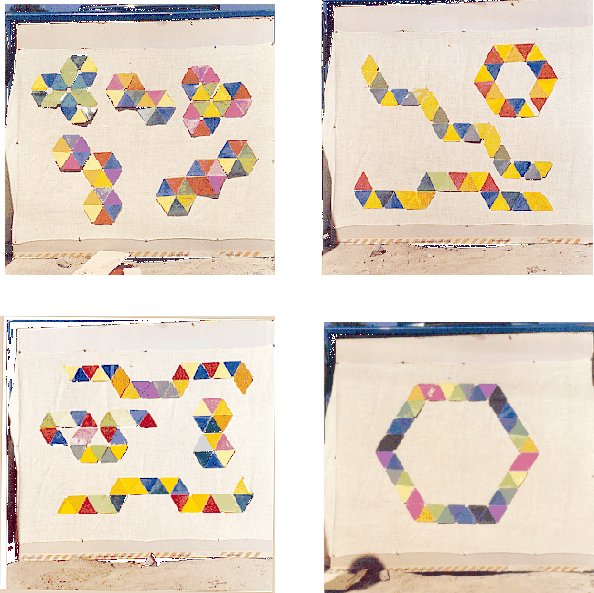 |
Generally speaking, if you have a lot of related items, it is a temptation to make a map showing their relationships. For example, in solving mazes (as early videogames like Mammoth Cave or Dungeons and Dragons typify, or more recent versions such as Myst exemplify) maps not only improve the tracing ability, but are practically indispensable. Differences in the arrangement of the flexagon were apparent, particurly in the thickness of the stacks running around its circumference. So the aim was to present this information in an easily comprehensible visual form.
Since the natural feel of a flexagon favors running through the same sequence of three faces over and over again, this can be described by a triangle with vertices labelled by the exposed number written on it for purposes of identification. Later on, coloring the faces and using the colors instead of numbers or letters has significant aesthetic appeal.
But the flexagon can be folded up or down, which can make a difference in the cycle by which the faces can be encountered. So there are triangles which have an edge in common (but not really). From the triangles it is a short step to the dual map, whose vertices are the triangles, represented by a dot in their center, and whose links show which triangles have an edge in common.
Actually, that is a face-dual, because there is an edge-dual in which the edges, also represented by a dot in their center, are linked according to whether or not they lie in sequence on a common triangle. Anyway, we didn't start thinking about edge duals until much later on, after having heard about the ``Tuckerman Traverse.'' So in summary, the most productive work with which I had a personal involvement was performed during the course of a few summers at RIAS, depending in good part on having the Princeton work gradually becoming available to supplement our own enthusiasm and insight, and in no small part on having some enthusiastic and resourceful people working together. Nevertheless, it always seemed that there were still quite a few loose ends, even though very little seems to have been done with them in the meanwhile.
It is hard to avoid a certain amount of historically oriented curiosity. Can it be that flexagons came into existence once ever solely as a consequence of the difference between the Continental A4 and the American letter size paper? Surely people have folded paper before; I remember making paper chains out of colored paper in grade school for Christmas tree decorations, and we all knew how to fold up paper and cut it so as to make five-pointed stars. Possibly it takes a certain mathematical viewpoint to appreciate simply turning strips of paper inside out over and over again. After all, flexagons have been patented ([28] and following references) as toys and amusement devices, yet we do not see them on sale in greeting-card stores.
There are two good contemporary sources of information about mathematical recreations. One of them is the Strens Collection1 at the University of Calgary in Edmonton, Alberta; the other is David Singmeister's compendium at the University of South London2 of which he distributed mimeographed copies and which has now been mirrored3 on the Internet. The latter, at least, does not show a great deal more published material on flexagons and the related flexatubes than that available in Conrad and Hartline's summary [20], although there are one or two items of recent provenance.
As for the original Princeton committee, it may well be that such a theory was not publishable in a mathematical journal, but was too voluminous and complicated to be published in a popular journal either. After all, reports concerning flexagons from elsewhere that did get published were short notes, and hardly of the length that a full treatment would have required. Nor is it probably the kind of material which would be appropriate for a doctoral thesis, being long on interesting examples and short on topological theory. Gardner's commentary was that in any event the war came along with other distractions. Still, even after sixty years, nothing seems to have captured the versatility and insight of the fragments that have been reported in what has survived of those efforts.
The work produced at RIAS was shown around, including to the individual members of the old Princeton committee, likewise without causing much excitement. What had begun as a high school project had to give way to the demands of college enrollment, so that much of the follow up required to get an article for a research level journal was never performed, perhaps becoming an example of history repeating itself.
In writing an introduction to [20] mention was made of possible applications to programming languages. We did not yet know about regular expressions nor Noam Chomsky's theory of language hierarchies, but we were actively learning about and working with John McCarthy's LISP, in which the parse tree for program instructions was just what was needed for flexagon layout. In those days compilers and programming languages were still a novelty, and it was considered a great accomplishment to be able to decipher formulas - something which algebra students did so easily.
To have an idea of what it is like to work with a flexagon, consider Figures 3 and 4, which show a variety of strips, painted and ready for folding. Of course, once the flexagon is folded up, the only thing which is visible is a painted hexagon, divided into six little triangles. One line of thinking decorates them with designs of one sort or another, but the more conservative approach is to simply paint them and let them be. However, part of the excitement, particularly when learning about flexagons for the first time, is the variety of serpents and coils and other shapes which the unfolded strip can assume.
The work sheet reproduced in Figure 5 has space for the map of the proposed flexagon, with a triangular network down below. The essential details to be remembered are that a long straight strip of triangles can be twisted clockwise around itself (say) to get a new straight strip, a process which can be repeated indefinitely. When first making flexagons, there is a tendency to measure off triangles carefully, even with the aid of instruments. However, if successive triangles are fan folded back on their predecessors, errors of judgement shrink by half, and the process converges nicely and is stable. However, if they are scroll folded, the accumulated thickness shortly becomes unmanageable, having doubled at each step.
Very well, that is how to prepare the strip; but to use it, it must be scroll folded. A flexagon is really defined by one third of the visible hexagon, so three identical sectors have to be prepared; of course that can be done from the outset by making the figure three times as long, by repeating one sector three times. This final cluster is what has to be bent into a moebius strip and the ends fastened together.
The point to be remembered is that long straight strips scroll fold, with a map which is a Cayley tree. If the process is carried to its recursive limit, the result is a Universal Flexagon, in the sense that any other flexagon can be derived from it by foregoing some of the hinges along edges of two successive triangles, which can be done by folding the hinge over and pasting the faces shut. Conversely, the covering space idea holds that if some finite flexagon won't fold, the face can be split in two leaving the new faces connected along an edge which is now a hinge. Then folding can be done, until the next futile attempt arises somewhere else.
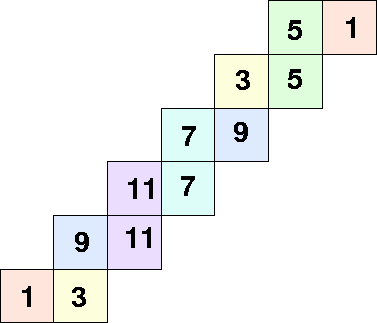 |
If enough faces of the Universal Flexagon are pasted, in the right places, the flexagon becomes accordion folded, and once flexed, won't flex again until it is turned over. But, thanks to the fan fold, the only penalty incurred by having a big flexagon is that there are huge stacks of paper, not that you can't raise one stack and lower the other, changing the face numbering or coloring (whichever) as you go along. But the strip which has to be fan folded is a pure spiral. We made one once; it was extremely cumbersome but it worked.
The difference between fan fold or scroll fold lies in whether the orientation of new triangles while running along the strip is always the same (scroll fold) or strictly alternates (fan fold). But that choice redounds in the Cayley tree, in terms of whether one heads left or one heads right while moving along, and so in whether one runs repeatedly around the same set of faces, or whether one heads off into the sunset. The latter generates the Tuckerman Traverse.
Having constructed, painted, and flexed numerous piles of paper, it became clear how to position spirals and straight strips practically at will, all the while foreseeing how the assembled flexagon would behave.
There is not all that much difference in understanding flexagons assembled from other polygons, such as the tetraflexagons built with squares. A square has more edges, consequently more hinge positions. the splitting used to derive a universal flexagon splits a face in three, not two, with a resulting uncertainty where the hinges sit - or rather, implied direction of folding - which is one source of the possibility of tubulation.
The principle of fan folding versus scroll folding still applies, affecting whether the consistent structures derived therefrom are spirals or straight line segments. Figure 6 shows the second stage approach to the universal tetraflexagon, which must be folded up from a diagonally running, but nevertheless essentially straight, strip of paper.
After lying dormant for nearly forty years, the work on flexagons got revived because of interest in the Internet. For several years I have been offering a graduate course in Cellular Automata at the Centro de Investigación y Estudios Avanzados which is part of the National Polytechnic Institute in Mexico City. Little by little we have been building up a Web site4 containing the text of articles which we have written and associated graphical material, including transcripts from the CAMail discussion group.
Besides the material strictly pertaining to cellular automata, there is a considerable residue from thirty years of teaching, social service projects, and thesis work to generate s substantial body of interrelated material. In particular, undergraduate theses are a requirement in the Mexican educational system; it has always seemed like a good idea to guide them towards the accumulation of results and expositions which would be of assistance in presenting course work. Given that they would be written in Spanish, students should find them easier to read than having to translate English articles and textbooks.
 |
Beyond that, there is much material left over from Aberdeen, Baltimore, and Florida, which could reasonably form part of the collection. As far as general interest goes, the Flexagon papers touch on a subject of wide popular appeal, namely Recreational Mathematics, so that their inclusion in the Web page should stimulate more consultation than the specialized work on group theory, quantum mechanics, or dynamical systems.
Even though it seemed like a simple project, it has taken the major part of a year to read the text optically and to copy the figures (the original drawings took their author and then the Martin Baltimore art department a fair amount of time to prepare them in the first place). While that was going on, they seemed to be sufficiently related to such things as automata and dynamical systems to look them over as part of the cellular automata course. Surprisingly enough (or perhaps not), the result was a much better understanding of their nature.
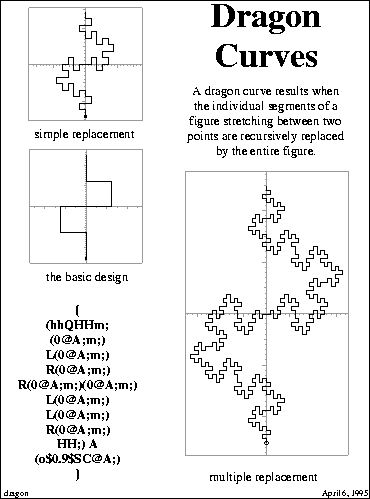
This understanding consists in regarding a flexagon as a geometric fractal, in the style of the dragon curves, and their predecessors such as Hilbert's space filling curve or Helga Koch's snowflake. Such figures result from replacing an arc, usually a line segment, by another figure, probably more complicated, some of whose internal arcs have been marked for further replacement. A true fractal replaces again and again without limit, but as a practical matter the fractal would only be carried through a few stages; interesting ways to partially fill up a plane region ensue. A construction for the classic dragon curve is reproduced in Figure 8.
A flexagon may be created from any polygon, although it is best to start with regular polygons, or at least suppose they are convex. The chosen polygon is itself a plane figure, but if a number of copies is stacked up with a slight separation between them, the assemblage has a third dimension, within which they may be rotated, reflected, translated, or moved about in some combation. We can call the polygons faces, to distinuish them from their edges, which will be used as hinges.
Now suppose that two consecutive faces on the stack have a pair of edges joined to make hinges, and that the edge selection rotates around the polygon so that the next free edge is always used. There will finally be a pair of edges, one on the bottom polygon and one one on the top polygon, that remain unconnected; in one's imagination they could be joined cyclically, but that would freeze the package and keep it from opening. Call the package, as yet unconnected, a sector.
At this point construct a second stack, turn it over, and connect its free edges to their counterparts in the first stack. Alternatively the original stack could have been twice as high, winding around twice, doubled over in the middle, and the extreme polygons hinged by connecting the remaining free edges. Using a double stack means we have matching hinges where we want them.
Two sectors have now been joined; laid out side by side. Supposing the polygons to have zero thickness, the configuration is planar, but with overlap. There is no reason not to work with three, four, or more sectors, and it will eventually be seen that sometimes this is desirable, but we have to wait a while to see where they will be needed.
The mirror symmetry of the pair of sectors assures us that trying to open up one stack by rotating a face around one of its hinges will be met by a matching opening in the other sector. The figure is now three dimensional, but its freedom of movement will be constrained by the angles between successive edges of the polygons. In the case of squares, the edges lie at 90° and the complex will open out into a larger square. With equilateral triangles, the complex can be opened, but not very far. Three sectors remedy this constraint, leading to Stone's original Moebius band.
For pentagons and higher order polygons the angular sum around the point of contact of the exposed polygons exceeds 360° keeping the ring from lying flat, but everything can still be coaxed into the required movements. If the ring is not flexible enough, this is the moment to incorporate additional sectors, taking care to open each sector in parallel with the others. The pieces of the individual sector which have been pulled apart are called pats5.
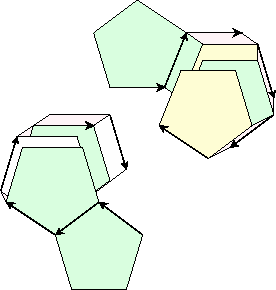 |
Altogether we have the terminal condition for a recursive definition, whose base consists of a ring of stacks of faces (the sectors). For normal flexagons, the number of polygons in each stack should equal their degree; they should be regular, and hinged at consecutive edges. Rotating the hinging sequence clockwise rather than counterclockwise will give an enantiomorphic flexagon. Doing many other things will still work, but they will lie outside the province of ``normal.''
The repetitive part of the recursive definition consists in replacing one of the polygons with an equivalent figure, one which admits of further substitution if desired. For a normal flexagon it is easy to find a suitable replacement. The main requirement is that the replacement connect pieces with the same angular orientation and displacement as before, so just drop one polygon from the stack and then turn the remainder over, as illustrated in Figure 9.
For pedagogical purposes, in order to understand the process clearly, it is a good idea to start with the primitive cycle, to be sure that it works, for all its simplicity and triviality. For triangles, with three sectors, Stone's band is the result. For squares, two sectors perform to specification, but the result is not the simplest tetraflexagon which Martin Gardner described in his second flexagon article [9], nor is it the double-acting hinge which is associated with barroom doors. Pentagons require a little maneuvering, familarity with which stands in good stead as one moves along to the higher polygons.
Once the primitive cycle is mastered, it is time to try substituting just one polygon, to get a binary flexagon. At first, bunching up the substituted stack with a paper clip helps to appreciate that the new wad is just one single face. Perhaps pentagons constitute an optimal illustration, given that a stack of four of them is thick enough to be noticed as a unit, yet the overall figure is still sufficiently small that its structure can be seen clearly. Such a flexagon was featured in Conrad's short paper [19].
Of course, more than one of the polygons in a sector can be replaced, yielding a wide variety of new flexagons. Some of them are mirror images of the others, and some of them may have more attractive behaviors than others. But the next pedagogical step is the second level flexagon, in which all the polygons have been replaced by their complementary stacks. For three sectored triangular flexagons, the result is Stone's discovery of the second day, that a strip of double the length could be wound up a little before proceeding to the Moebius band. It is also what I originally called ``face splitting.'' Second level tetraflexagons are the ones described in Figures 6 and 7. but they don't seem to appear in any of Martin Gardner's discussions, most of which seem to rely on some other principle for creating the things he calls tetraflexagons [11,13]; see [26].
 |
Second level flexagons for higher polygons are increasingly complicated and cumbersome, yet still accessible to construction performed with care and patience. Beyond the second level liee a third order, and so on. Constructing them would probably be the result of obstinacy more than anything, but getting to third and even fourth order with equilateral triangles is not unreasonable.
The maps, and the Tukey Triangle strips, which were so useful for planning out triangular flexagons, persist for higher polygons. But rather than starting from them as bases for definitions, it seems to be easier to get them by the same recursive process by which the flexagons themselves are constructed. In other words, an edge which is part of a cycle in the Tuckerman Tree gets replaced by a tangent cycle of its own during the recursion. The Tukey polygon strips gets altered by the same process, exactly as does Oakley and Wisner's permutational flexagon definition.
Whether the cycle should be of the same length can lead to a discussion of mixed flexagons, but for a normal flexagon equality is a requirement. Once the normal flexagons have been established, any number of variants come to mind, beginning with relaxing the building rules of the primitive stack to include other polygons besides the regular ones, oe even foregoing the assumption that they are all equal. Something really exotic would be extending the fractal paradigm6 to three dimensions, accepting that rotating and flexing in the fourth dimension can only be contemplated; just the end results can be visualized.