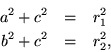


Next: A projective version
Up: The circle of intersection
Previous: The circle of intersection
Contents
Suppose that circle i has radius 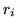 , that
, that 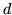 is the distance between
centers, and that we form a plane section including the two centers and
is the distance between
centers, and that we form a plane section including the two centers and
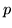 , one of the points where the circles intersect. Let the perpendicular
from
, one of the points where the circles intersect. Let the perpendicular
from 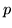 to the line joining centers have length
to the line joining centers have length 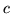 while dividing that
line into segments of length
while dividing that
line into segments of length 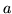 and
and 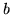 . By the Pythagorean theorem,
. By the Pythagorean theorem,
whence we conclude
At the same time,
Manipulating these last two equations gives forms for 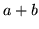 and
and 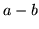 which
in turn yield
which
in turn yield
the formula for 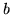 results from exchangiong
results from exchangiong 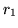 and
and 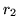 . Interestingly,
the spheres need not even intersect, but then
. Interestingly,
the spheres need not even intersect, but then 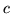 would be imaginary:
would be imaginary:
Pedro Hernandez
2004-05-13
![]() , that
, that ![]() is the distance between
centers, and that we form a plane section including the two centers and
is the distance between
centers, and that we form a plane section including the two centers and
![]() , one of the points where the circles intersect. Let the perpendicular
from
, one of the points where the circles intersect. Let the perpendicular
from ![]() to the line joining centers have length
to the line joining centers have length ![]() while dividing that
line into segments of length
while dividing that
line into segments of length ![]() and
and ![]() . By the Pythagorean theorem,
. By the Pythagorean theorem,