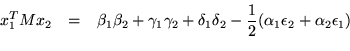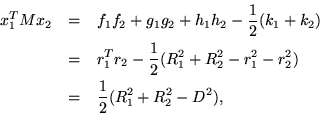


Next: A general procedure
Up: The circle of intersection
Previous: Trigonometric solution
Contents
Recalling that the equation of a sphere is
regard the coefficients as a vector in a five dimensional space.
Because any non-zero multiple of the equation defines the same sphere,
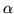 may as well be chosen equal to 1 unless it, itself, is zero.
Except for this degenerate case, substituting
may as well be chosen equal to 1 unless it, itself, is zero.
Except for this degenerate case, substituting
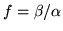 ,
,
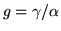 , and
, and
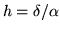 gives a vector
gives a vector
with r the center of the sphere. Similarly, set
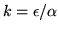 to get
to get
when 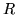 is the radius of the sphere and
is the radius of the sphere and 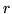 the distance between its
center and the origin.
the distance between its
center and the origin.
Defining a metric matrix
creates an inner product for which, given coefficient vectors
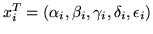 ,
,
If it were agreed to use normalized vectors
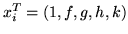 , we would
have instead,
, we would
have instead,
The last two lines result from normalizing the vectors; the very last
is a consequence of the cosine law and calling 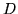 the distance between
centers. According to this, the norm of a sphere is its radius, no matter
where it sits.
the distance between
centers. According to this, the norm of a sphere is its radius, no matter
where it sits.
Some further trigonometry produces the most interesting version of the
formula,
wherein 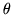 is the angle at which the two spheres intersect, taken to
be the angle between their tangent planes at the point of intersection.
This is the same as the angle between the normals to the surface, which
are themselves radii.
is the angle at which the two spheres intersect, taken to
be the angle between their tangent planes at the point of intersection.
This is the same as the angle between the normals to the surface, which
are themselves radii.
The remarkable conclusion is that orthogonal circles are those which
intersect orthogonally, just as parallel or antiparallel circles are
those which are tangent at their intersection. Parallel means internally
tangent, antiparallel means externally tangent.



Next: A general procedure
Up: The circle of intersection
Previous: Trigonometric solution
Contents
Pedro Hernandez
2004-05-13
![]() may as well be chosen equal to 1 unless it, itself, is zero.
Except for this degenerate case, substituting
may as well be chosen equal to 1 unless it, itself, is zero.
Except for this degenerate case, substituting
![]() ,
,
![]() , and
, and
![]() gives a vector
gives a vector
![\begin{eqnarray*}
M & = & \left[ \begin{array}{ccccc}
. & . & . & . & -1/2 \\ ...
...& . & . & 1 & . \\
-1/2 & . & . & . & .
\end{array} \right].
\end{eqnarray*}](img54.gif)