Several different graphs, and kinds of graphs, turn up while describing flexagons and trying to organize their properties. To begin with, there is the layout of the flexagon, for which there are two points of view. One is that is a polygon stack, members of which are joined by edges, yet forming a single sequence. That means each polygon is joined to a successor, and that a predecessor was joined to it, along a separate edge. No other polygons are connected to it than these two. It took a while to see that this configuration was essential to the definition of a flexagon.
The other view that one gets is that of a long chain of polygons meandering around in a plane. There may be subconscious objections to letting it cross over itself but these are easily overcome. It just complicates constructing the flexagon because then it has to be laid out in layers. Such chains are called friezes, which is an architectural word referring to the stripe usually placed in a room to separate the wallpaper covering the walls from that covering the ceiling; but also to the space between the walls and roof in a temple or building. In that context the overlapping never comes up, of course.
Laying out a frieze, there is no reason to work from a single polygon prototype nor to obtain its neighbors by reflecting in an edge, although it is clear enough that the resulting stack is uniformly built from the same polygon, turned over if need be, and connected by two different edges to its neighbors.
There is no reason to think that a frieze has to be overlaid on a lattice, and in fact squares and equilateral triangles are about the only polygons from which a grid can be formed. Nevertheless, those two polygons are so frequently used to make flexagons that it is often convenient to prepare paper on which the friezes can be drawn. This is true whether the frieze is to be cut out from the drawing, or the drawing is to be filed away to preserve the shape of the frieze for future reference.
Such graphs are concerned with physical construction of the flexagon. Others summarize their properties abstractly, but are nevertheless worthwhile for just that reason; they are maps of the flexagon's behavior. Again we have seen two different graphs, and how one is nestled inside the other. Someone given a flexagon and told how to manipulate it would probably want to diagram the possibilities. The most visible property of the flexagon is the set of faces which are visible when it is held in the hand or laid down on a tabletop. To distinguish one set from another, they can be marked. Painting all the exposed surfaces is an artistic way to do this, whereas writing letters or numbers will result in a better mathematical description, especially the use of numbers.
The basic operation is that of flexing, which means moving some constitutent polygons from one part of the figure to another. As an entirely new set of surfaces will become visible, they ought to have a new color or number as the circumstances dictate. The main choice in flexing lies in making valley folds or in making mountain folds. That gives two choices for exposing the colored sets, which we may well just call faces. That is reminiscent of the two neighbors seen while looking at the frieze, but these are abstract neighbors which can be marked as points on a map and connected by lines according to whether they can be exibited relative to one another by flexing.
Instgead of talking about mountain and valley folds, it is possible to concentrate on one kind of fold and change to the other by rotating the flexagon. That means that instead of linking points by ``valley'' and ``mountain'' they would be linked by ``flex'' and ``rotate,'' taking into account that ``rotate'' doesn't change any colors. This can all get fairly confusing in the lack of practice and expecially in the absence of exact definitions.
Nevertheless by persisting it is gradually observed that some operations on the flexagon run through cycles, and that other operations result in changing the cycles, although you can't change cycles forever, and that they can only be changed in certain sequences. That is what makes flexagons good entertainment devices - having to figure out all the relationships. Not in the construction, which is another issue, but in their usage and their external appearance.
Close observation relates the internal structure to the external structure. The cycles correspond to three dimensional movements of the polygon stack, especially of removing a polygon from the top of one stack and placing it on the bottom of the neighboring stack, recalling that the stack is arranged as turns of a spiral and that two or more of these turns get laid out flat to form the visible flexagon.
The choice of fold types becomes possible when individual polygons are replaced by whole structures - single counter turns or the result of a whole series of such substitutions - and the unfolding and transfer is made in one of these structures rather than in the original spiral. That is the recursive step which allows one to call a flexagon a ``fractal polygon stack'' and compare it with other objects built up by similar procedures.
The sequence of substitutions can be carried out in varying degrees in any flexagon to get another, new, flexagon, and considerable effort has gone into cataloging all the possibilities. Or at least as many of them as practicality and patience permits. When we were first studying flexagons there was an effort to build as many different ones as possible so as to be able to compare them and try to capture the essence underlying them. Now that the interplay of fundamental cycles and substitution is better understood, interest lies more in finding nice illustrative examples or in especially educational combinations. In any event, placing large numbers of polygons on top of one another places mechanical limitations on an otherwise limitless construction.
The third diagram is the first one which we constructed, although we never knew the sequence followed by this Princeton Flexagon Committee except for the fact that Stone came across the use of multiple doubling right away, according to Martin Gardner. It is a natural enough discovery; one wonders when tripling was first revealed as the essential operation for square flexagons.
The diagram uses points for cycles, and connects cycles which have faces in common. Precisely, the color on top of the flexagon and the color on the bottom. It may or may not be possible to switch cycles, but if it is it is by folding ``up'' or ``down,'' which is equivalent to ``mountain'' or``valley.'' To make an example, suppose that we want three cycles in a certain kind of square flexagon, and that they should be connected according to the following diagram:

The best way to procede mathematically would be to draw the diamonds, although historically squares representing the cycles would have been drawn first. To shorten the time to make the drawing, they can both be drawn at the same time.
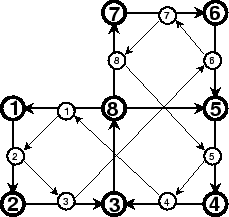
That will result in a list of eight labels (with a ninth for connecting)
| + | + | + | + | + | + | - | - | + |
| 1 | . | 3 | . | 7 | . | 5 | . | 1 |
| . | 2 | . | 6 | . | 8 | . | 4 | . |
which would be completed by adding 1's,
| + | + | + | + | + | + | - | - | + |
| 1 | 3 | 3 | 7 | 7 | 1 | 5 | 5 | 1 |
| 2 | 2 | 4 | 6 | 8 | 8 | 6 | 4 | 2 |
Finally the frieze, or rather half of what is needed, would be
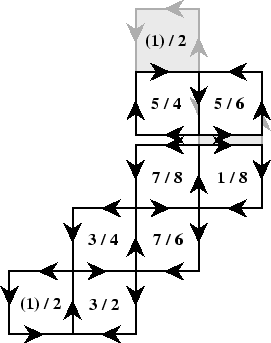
This is an example of a process which can be carried out in great variety, and which should be done with enough examples that one is fairly sure of how the construction goes.
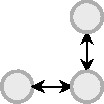
The map for the binary flexagon would simply be
whereas for the second level flexagon it becomes
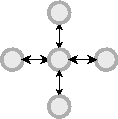
To get to the third level,
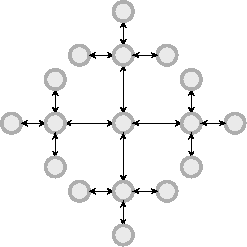
although I don't think we have ever made one of these and gotten it to flex, the folded paper having gotten so thick that operation became unmanageable. More levels keep adding little crosses to the arms of the crosses which are already there, but the congestion would be all that much worse if anyone tried to make the flexagon.