Although flexagons were discovered by folding long strips of paper into closed loops, it turns out that the best way to think of them is in terms of stacks of identical polygons folded back and forth over each other and then closing the ends together so that they will fold out in three dimensional space. In other words, polygon stacks versus folded friezes; it is interesting how a change in viewpoint can make all the difference in interpretation. Or at least in visualizing the proces.
At first the stack is fanfolded from polygons connected edge-to-edge in succession. Before trying out skipping edges or occasional scroll folding, it is interesting to replace a polygon by a counterstack, which consists of a spiral turned over so that the angle between edges is the same as it was before. By experimenting it can be verified that clumping the counterspiral together as a single entity changes nothing except that a fatter polygon with internal structure has been used. It could be glued together on all faces and that would be quite literally true. Conversely it could be thought that the first polygon had been sliced up salami fashion, except the pieces were still partially joined.
In fact, that is how we thought of complicating Stone's original triangle flexagon, except that it didn't occur to us that with squares you needed three slices rather than two and that the connecting edges had to rotate around the square. Later the idea caught more attention, but apparently never got elaborated and formalized to the extent that it should have. Besides, it is helpful to transfer the idea to the maps and face lists, but we only knew about those as recipes that worked and weren't too sure how they were derived. Since the Flexagon Committee never wrote up a report, doubts remain as to how they finally evolved the process that was discussed here and there.
Even now, the concept of replacing a point on the cycle map by a tangent cycle running in the opposite direction seems to be something which is more justified by the fact that it seems to work than by any rigorous geometrical deduction.
This is a distinction which is often missed in geometry classes and by people who are either too rigorous or insufficiently rigorous. To say that geometry is a collection of ``obvious'' facts misses what seems to have been Euclid's objective, which was to show the interrelationship of all those facts, and to show that they could be built up in an orderly progression starting from relatively few basic assumptions. So just as the geometry teacher who won't let the students draw pictures is depriving them of a helpful visualization and memory aid, those students who feel that by drawing a picture, they have proved something, have erred in the other direction. One needs to know, Why?
With flexagons the situation isn't so drastic, because a whole branch of science doesn't depend on it. Still, what one is looking for is a model which, while not as complicated as the object it is describing, captures its essential properties, describes it, and allows predictions. So it would be possible to do flexagons by analytic geometry, assigning all the points coordinates, and writing formulas for reflections, rotations, and the other operations. People do something pretty much like this when the model structures in civil engineering, and the people at Industrial Light and Magic do it when they sumulate dinosaurs running across the field and jumping over logs.
Even without the algebra and computation, we have had several people try their talents as artists in drawing flexagons and showing clearly the operations. It is more complicated than one would think; all the more so before the best line of reasoning was apparent. Now that we have nice video cameras, we have been thinking of showing the process by actual example without the drawing. We may actually get around to doing it.
In the meantime, ``what has been done once, can be done again,'' as the explanation of mathematical induction goes. Having understood the principle of substitution, there is no reason not to go on and on, substituting here and there. Some sequences of substitution produce interesting designs, and much of our early work was dedicated to making them, in hope of grasping a general principle. But it is still worth the effort to advance in an orderly fashion, an example of which would be to replace every polygon in a primary spiral by a counterspiral, to get a second level flexagon. Replacing each of those in turn would lead to the third level, and so on.
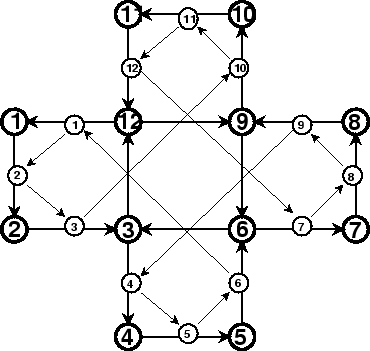
For squares, and again working with a single blade of the flexagon while understanding that in the end several (say two) will be required, each of four squares will be replaced by three, which means a total of twelve. The two interleaved maps, of visible colors and of the polygon positions, will look like this:

In the ASCII script, only the diamonds were labelled, and since there aren't any diagonal arrows in ASCII, they would have to be drawn in over the printed page. Note that all turns are in the same direction, which can be counterclockwise, so that the three line list of labels for the squares will read
| + | + | + | + | + | + | + | + | + | + | + | + | + |
| 1 | . | 3 | . | 11 | . | 7 | . | 9 | . | 5 | . | 1 |
| . | 2 | . | 10 | . | 12 | . | 8 | . | 4 | . | 6 | . |
before adding 1 to the numbers to get the number opposite. That can also be done on a printed copy. The required frieze will be made from squares joined along consecutive edges, so it will look like the strip we have used before, only longer.
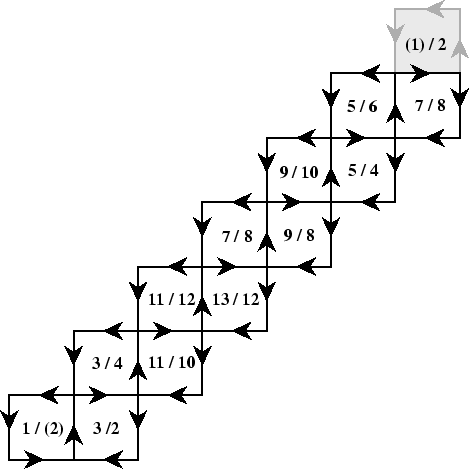
This is half the flexagon; another copy is needed, to be joined with this one.
As a general proposition, all second level flexagons will look like the first level flexagons, except for the fact that some segments could be folded up first to get a strip which looks exactly like the first level strip, according to which the remainder of the folding would be the same as before.
For triangles, there is a natural temptation to give additional twists to the triangle strip before closing it into a hexagon, which is how Arthur Stone discovered them right away. For squares, the strip isn't quite as natural, and it is necessary to pause after folding three squares to fold the next three, and then fanfold those before going on to the next group. Pentagons work the same way, save that the secondary groups have four pentagons; and so on for any other polygon with more sides.
All the variety will doubtless seem very confusing, which is why it is mportant to organize the work in stages and procede step by step.