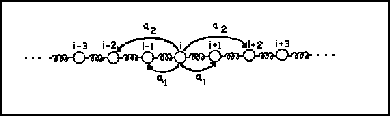

Analizando esta gráfica vemos que el coeficiente ``![]() ''
depende de la interacción entre la masa
''
depende de la interacción entre la masa ![]() y su segunda vecina por
la derecha más próxima, esto es la
y su segunda vecina por
la derecha más próxima, esto es la ![]() ; pero este coeficiente
debe ser el mismo en la otra dirección, debido al modelo uniforme
que adoptamos, esto es, la interacción con la segunda partícula
por la izquierda más próxima; esta misma consideración se aplica
al coeficiente ``
; pero este coeficiente
debe ser el mismo en la otra dirección, debido al modelo uniforme
que adoptamos, esto es, la interacción con la segunda partícula
por la izquierda más próxima; esta misma consideración se aplica
al coeficiente ``![]() '' que resulta de interacciones a primeros
vecinos, esto impone una uniformidad. Esta uniformidad es consecuencia
de las leyes de Newton que involucran la simetría de fuerzas, y
también de la homogeneidad de la cadena, por lo tanto es un
resultado en el que se puede confiar físicamente.
'' que resulta de interacciones a primeros
vecinos, esto impone una uniformidad. Esta uniformidad es consecuencia
de las leyes de Newton que involucran la simetría de fuerzas, y
también de la homogeneidad de la cadena, por lo tanto es un
resultado en el que se puede confiar físicamente.