Further variants

**Figure 12:** Stability surface for the relativistic Mathieu potential with a sharpening third harmonic.
$\begin{figure} \centering \begin{picture} (400,150) \put(0,-40){\epsfxsize=400pt \epsffile{sharp3dhview.eps}} \end{picture} \end{figure}$

**Figure 13:** The relativistic Mathieu potential sharpened by its third harmonic.
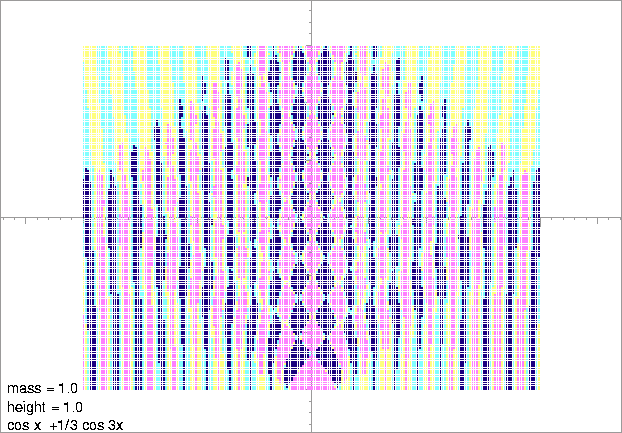$\begin{figure} \centering \begin{picture} (400,270) \put(0,0){\epsfxsize=400pt \epsffile{sharp3dhcont.eps}} \end{picture} \end{figure}$

**Figure 14:** Stability surface for the relativistic Mathieu potential with a flattening third harmonic.
$\begin{figure} \centering \begin{picture} (400,160) \put(0,-40){\epsfxsize=400pt \epsffile{flat3dhview.eps}} \end{picture} \end{figure}$

**Figure 15:** The relativistic Mathieu potential flattened by its third harmonic.
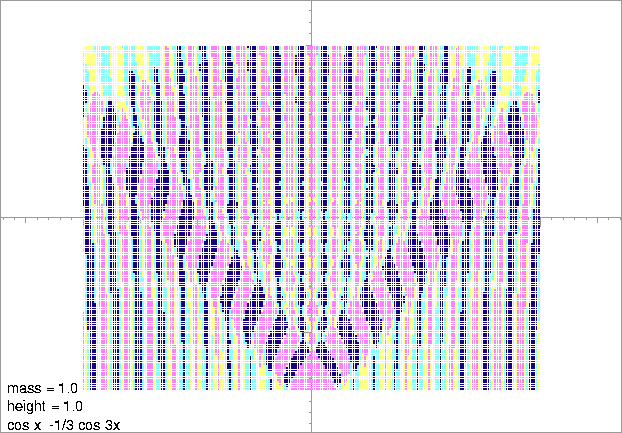$\begin{figure} \centering \begin{picture} (400,300) \put(0,0){\epsfxsize=400pt \epsffile{flat3dhcont.eps}} \end{picture} \end{figure}$

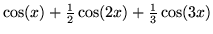**Figure 16:** Stability surface for the relativistic Mathieu potential with a delta-function-approximating potential $\cos(x)+\frac{1}{2} \cos(2x)+\frac{1}{3}\cos(3x)$ .
$\begin{figure} \centering \begin{picture} (400,300) \put(0,-20){\epsfxsize=400pt \epsffile{deltaview.eps}} \end{picture} \end{figure}$

**Figure 17:** Terms in the coefficient matrix plus one solution for the potential $\cos(x) + \cos(2x) + \cos(3x)$ . The potential is fairly flat on the bottom with a dent, while on top the peak approximating the delta function is quite conspicuous. The result is that negative energy solutions see a mild reflecting corrugation while positive energy solutions see an ever rising barrier through which they can tunnel.
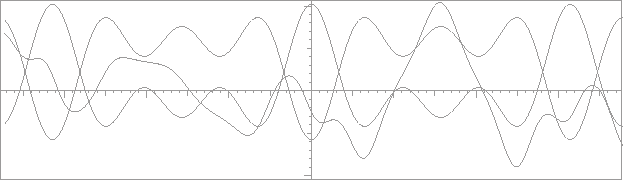$\begin{figure} \centering \begin{picture} (400,110) \put(0,0){\epsfxsize=400pt \epsffile{deltagraf.eps}} \end{picture} \end{figure}$

**Figure 18:** Contour map for the relativistic Mathieu potential with a delta function approximating potential $\cos(x) + \cos(2x) + \cos(3x)$ . The squares outline the regions whose perspective view is shown in Figure 16.
$\begin{figure} \centering \begin{picture} (400,300) \put(0,0){\epsfxsize=400pt \epsffile{deltacont.eps}} \end{picture} \end{figure}$

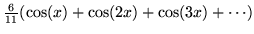Finding a relativistic version of the Kronig-Penney model has created some consternation in the physics literature. The contour map of Figure 18 shows the result of approximating the delta function by the Fourier series $\frac{6}{11}(\cos(x) + \cos(2x) + \cos(3x) + \cdots)$ . A notable discrepancy develops between solutions with negative energy and those of positive energy.

Although the average potential in this approximation is zero, it reaches an appreciable maximum while retaining a minimum close to zero. After all, that is the desired result, but the environment which it presents to wave functions of opposite energies is quite different. Instead of a similar mass shell for the two alternatives, the shell has a negligible presence around the high peaks, while constituting a uniform barrier along its base.

The mass-dominated region in Figure 18 rises at a high angle on the left because of the relation of the factor 6/11 in the potential definition to the step size in the contour plotter. effects can be seen on the right but they are barely visible.