First Level Pentagonal Flexagon

**Figure 1:** The full first level pentagonal flexagon has 5 vertices.
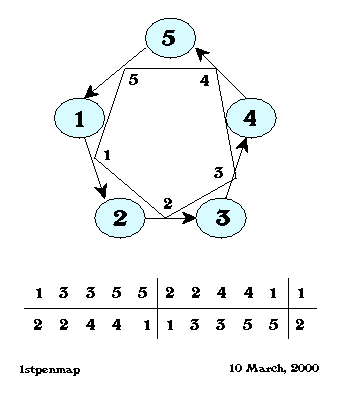
$\begin{figure} \centering \begin{picture} (250,275) \put(0,0){\epsfxsize=250pt \epsffile{1stpentmap.eps}} \end{picture} \end{figure}$

Flexagons constructed from regular pentagons are instructive in many respects. Unlike flexagons constructed from squares or triangles, the figure does not lie flat in the plane. Notwithstanding their nonplanarity, single cycle flexagons whose central angle sum exceeds 360° can always be run through their cycle even when they can't be laid out flat, so that the principle which bases a flexagon on a stack of polygons can always be confirmed.

Pentagon flexagons are good for observing that any number of leaves may be taken out of one pat and placed in the other. Single leaves give a figure anchored on the vertices of the pentagon, but taking two leaves gives a result which looks like tubulation, since it is anchored on the prolongations of edges surrounding the one which was skipped. With squares, that makes an exact tubulation.

Skipping three leaves forward looks like skipping two backward which is akin to folding the flexagon backwards. However, for polygons with a large number of sides, small numbers of leaves may be grasped simultaneously to advance rapidly around the cycle of faces.

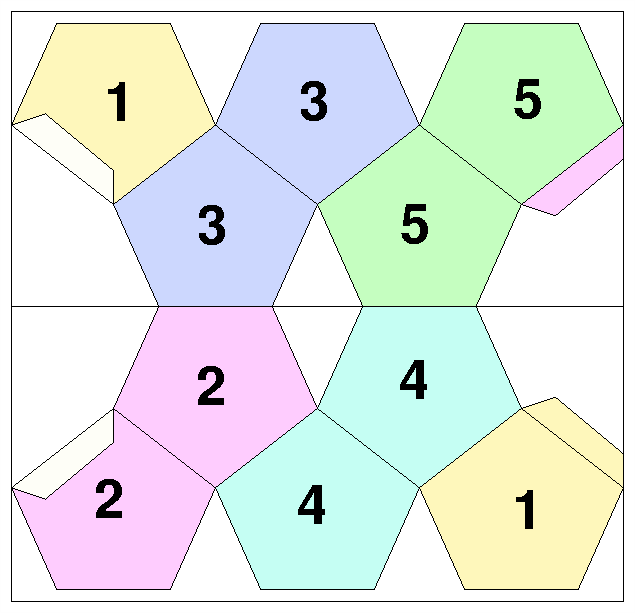
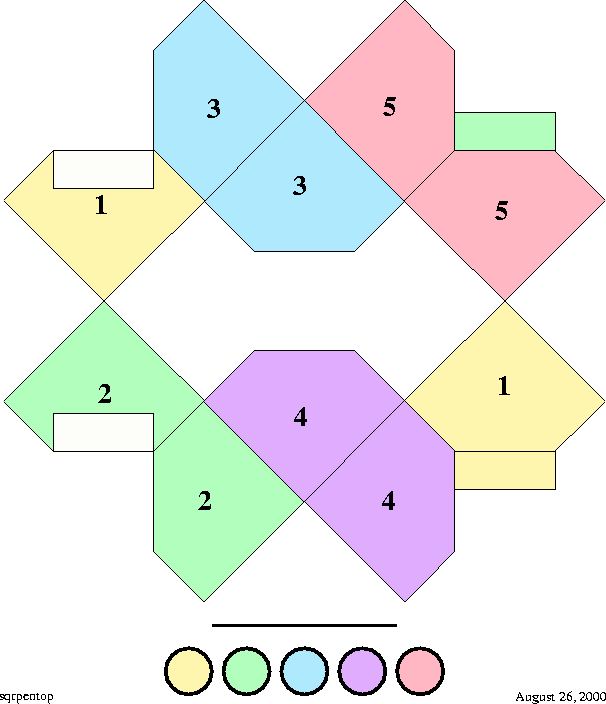
The inductive part of the construction, which allows the substitution of a single polygon for an inverted stack spanning the same angle is most readily confirmed with the binary flexagon, wherein one single polygon has undergone this replacement. A stack of four pentagons is sufficiently thick as to be noticeable as an entity, and requires sufficient exertion to run through either one of the two cycles that it probably illustrates the principles of flexagons better than some other choice. A stack of two triangles is rather inconspicuous, while three squares have too much in common with coordinate axes and smooth folding to be entirely convincing. Pentagons do nicely, avoiding the ever thicker stack which results when the number of sides of the polygon is increased. Still, binary flesagons of all orders illuminate the principles of flexagon construction.

Much of the excitement of exploring flexagons resulted from the multitude of was in which triangle flexagons as well as square flexagons could be compounded by adding new cycles to the Tuckerman traverse. Of course, all the other polygons offer the same possibilities, each time with a greatly increased scope of alternatives. A more systematic approach would be to replace all the polygons in the basic cycle with inverted stacks, arriving at what one might call the second level of flexagon. Working along similar lines would lead to third level flexagns, fourth level, and so on. All can be prepared from winding up previously prepared polygon strips, but the thickness of a paper implementation rapidly makes physical realization difficult and then impossible.

**Figure 2:** Permutation of the pentagons along the strip for a first level Pentagonal Flexagon.
$\begin{figure} \centering \begin{picture} (100,100) \put(0,0){\epsfxsize=100pt \epsffile{pen1levper.eps}} \end{picture} \end{figure}$

**Figure 3:** Top side of a Pentagonal Flexagon consisting of a single cycle. The figure should be cut horizontally through the middle, and one tab pasted to match colors. Once the figure has been folded up, the other tab should be pasted where space for it has been provided. The flexagon will not lie flat, but the two sectors will divide easily into twp pats each, within which leaves can be separated and moved from one pat to the other by flexing.
$\begin{figure} \centering \begin{picture} (406,406) \put(0,0){\epsfxsize=406pt \epsffile{pen1top.eps}} \end{picture} \end{figure}$

**Figure 4:** Bottom side of a Pentagonal Flexagon consisting of a single cycle.
$\begin{figure} \centering \begin{picture} (406,406) \put(0,0){\epsfxsize=406pt \epsffile{pen1bot.eps}} \end{picture} \end{figure}$

**Figure 5:** Top side of a squared up pentagonal flexagon. In this figure there are three 90° angles and two 45° angles, but the figure resembles a house with a peaked roof because two of the right angles raise the walls off the floor, while the third sits up in the gable.
$\begin{figure} \centering \begin{picture} (390,510) \put(0,0){\epsfxsize=390pt \epsffile{sqpentop.eps}} \end{picture} \end{figure}$

**Figure 6:** Bottom side of a squared up pentagonal flexagon.
$\begin{figure} \centering \begin{picture} (400,490) \put(0,0){\epsfxsize=400pt \epsffile{sqpenbot.eps}} \end{picture} \end{figure}$

**Figure 7:** Top side of a lopped off square pentagonal flexagon. In this figure there are three 90° angles and two 45° angles, but the figure resembles a lopped off square because the three right angles run in sequence.
$\begin{figure} \centering \begin{picture} (400,440) \put(0,0){\epsfxsize=400pt \epsffile{sqrpentop.eps}} \end{picture} \end{figure}$

**Figure 8:** Bottom side of a lopped off square pentagonal flexagon.
$\begin{figure} \centering \begin{picture} (400,440) \put(0,0){\epsfxsize=400pt \epsffile{sqrpenbot.eps}} \end{picture} \end{figure}$