Next: Binary Pentagonal Flexagon Up: Pentagonal Flexagons Previous: First Level Pentagonal Flexagon

First Level Pentacle Flexagon

**Figure 9:** The full first level Pentacle Flexagon has 5 vertices.
$\begin{figure} \centering \begin{picture} (250,275) \put(0,0){\epsfxsize=250pt \epsffile{pen++map.eps}} \end{picture} \end{figure}$

The pentacle flexagon works out well because of the cancellation of two conflicting tendencies. The angle between two consecutive pentagons joined by skipping an edge is too large to accomodate the mountain fold - valley fold transition which is sometimes necessary, but by taking two leaves together to make the flex, the fourfold angle reduces modulo 360° to the normal angle for a pentagonal flexagon, so flexing may procede without incident.

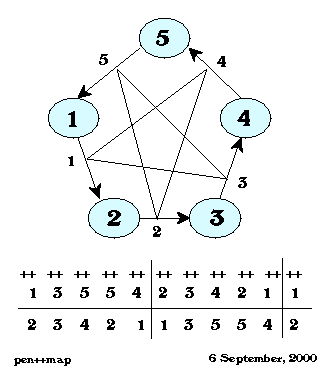
**Figure 10:** Permutation of the pentagon labels along the strip for a first level Pentacle Flexagon.
$\begin{figure} \centering \begin{picture} (100,100) \put(0,0){\epsfxsize=100pt \epsffile{pen++per.eps}} \end{picture} \end{figure}$

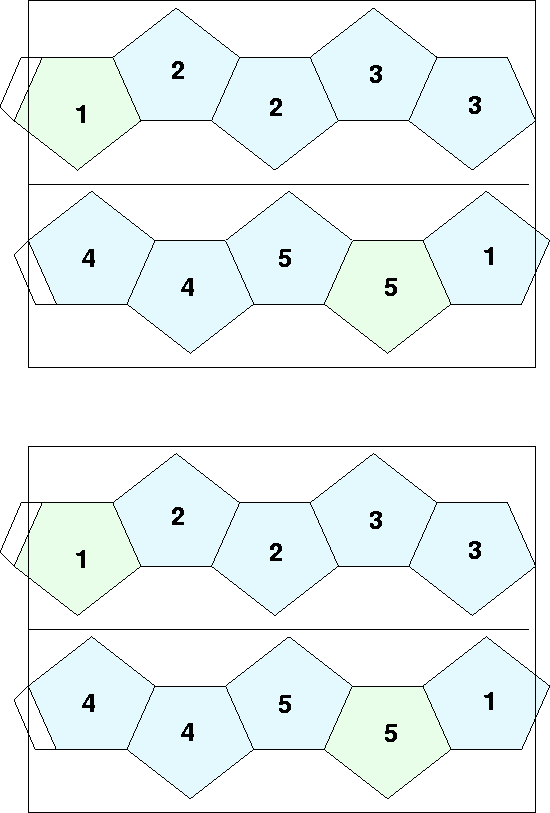
**Figure 11:** Top side of a Pentacle Flexagon. The pentagons are joined, not by consecutive edges, but by skipping an edge. Five pentagons comprise one sector, a minimum of two of which are needed for a flexagon. Thus sufficient material is shown for two minimal flexagions.
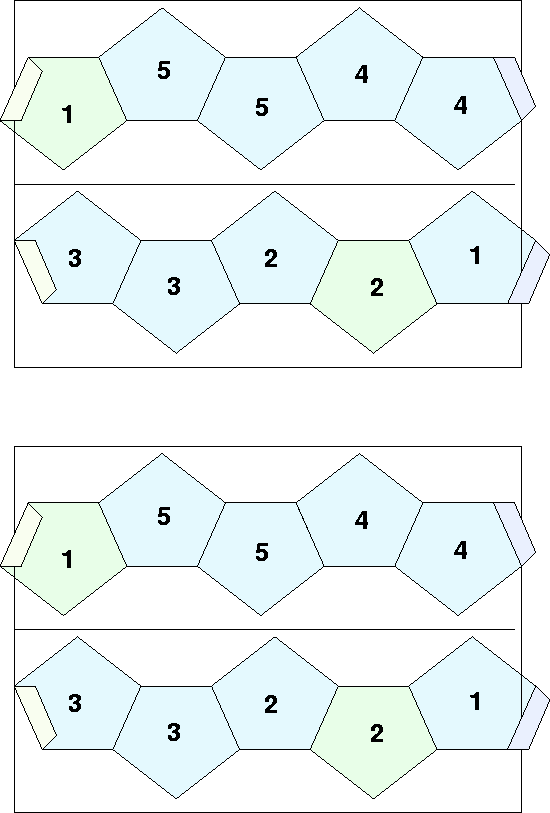$\begin{figure} \centering \begin{picture} (350,525) \put(0,280){\epsfxsize=350pt... ...} \put(0,0){\epsfxsize=350pt \epsffile{pen++top.eps}} \end{picture} \end{figure}$

**Figure 12:** Bottom side of a pentacle flexagon.
$\begin{figure} \centering \begin{picture} (350,520) \put(0,280){\epsfxsize=350pt... ...} \put(0,0){\epsfxsize=350pt \epsffile{pen++bot.eps}} \end{picture} \end{figure}$

Next: Binary Pentagonal Flexagon Up: Pentagonal Flexagons Previous: First Level Pentagonal Flexagon

Microcomputadoras
2000-10-02