Spectral Density

Supposing that a and b are both finite, defining an interval in which p is not zero and q is not singular, we can suppose that the Sturm-Liouville system exists for that interval. Thus there is a sequence of eigenfunctions $\psi_i$, with eigenvalues $\lambda_i$, which allows the expansion of an arbitrary function f:

$$\begin{eqnarray*}f(x) & = & \sum_{i=0}^\infty c_i\psi_i, \end{eqnarray*}$$

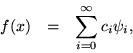
The completeness of such a basis $\{\psi_i\}$ can be exhibited through the general validity of Parseval's equality

$$\begin{eqnarray*}\int_a^b\vert f(x)\vert^2dx & = & \sum_{i=0}^\infty\vert c_i\vert^2, \end{eqnarray*}$$

which we can write in the more symbolic form

$$\begin{eqnarray*}(f,f) & = & \sum_{i=0}^\infty\vert(\psi_i,f)\vert^2, \end{eqnarray*}$$

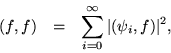
Now, use the bracket to evaluate these inner products:

$$\begin{eqnarray*}\frac{1}{\lambda-\lambda^*}\{[f,f](b)-[f,f](a)\} & = & \sum_{... ...psi_i(b) - [f,\psi_i](a)\vert^2}{\vert\lambda-\lambda_i\vert^2}, \end{eqnarray*}$$

The point is that all expansion formulas use parentheses, which we can turn into brackets at will by using Green's formula.

To simplify this expression we should like to nullify its dependence on the point b, and to standardize its dependence on the point a. Independence from b will be particularly important in taking the limit as the right endpoint recedes to infinity. Although the elimination of b cannot be achieved for all functions f, we can commence by selectively applying the formula to functions lying in the null space of the bracket at the right endpoint. We have already seen that this leads to the Titchmarsh-Weyl m function, and will moreover leave the left-hand side of the equation free of an explicit dependence on b.

Removal of b from the right-hand side of the equation can be accomplished by the selection of the boundary conditions which the Sturm-Liouville eigenfunctions are to satisfy, which could include the requirement that their brackets with f (or its real and imaginary parts) vanish. While it is necessary to verify that we are at liberty to make such a requirement, we nevertheless have the means of removing the explicit dependence on b from the right-hand side of the equation.

Standardization of the form of the right-hand side at the left-hand boundary point a can be accomplished by employing the remaining Sturm-Liouville boundary conditions together with the arbitrariness still resident in the definition of the m function, that it is the coefficient of only one of the initial-value basis functions.

Weyl's line of reasoning was to insist that the function f meet a real boundary condition at b, which of course ensures that [f,f](b)=0. Then he required that the Sturm-Liouville system meet the same boundary condition as f, which is tantamount to requiring that

$$\begin{eqnarray*}[f,\psi_i](b) & = & 0, \end{eqnarray*}$$

To meet the corresponding requirement at a, we require that $\psi$ satisfy a real initial value, and that

$$\begin{eqnarray*}[\psi,\psi_i](a) & = & 0, \end{eqnarray*}$$

so that

$$[f,\psi_i](a) = [\varphi,\psi_i](a) = r_i.$$

This proportionality constant r_i, has the significance that the initial-value basis function $\psi$ starts out from a unitary initial value in the boundary value space, so that $[\varphi,\psi] = 1$, while the basis functions $\psi$, are normalized to unity in the Hermitian metric in the solution space $(\psi_i,\psi_i) = 1$ Then r_i has the significance that it is the initial amplitude of a real normalized solution of the differential equation over the interval $a,\ b$. When we are dealing with a continuum wave function which has an asymptotically constant amplitude, a quick way to obtain this proportionality is to solve the initial-value problem with unit initial amplitude, then take the reciprocal of the asymptotic amplitude. The actual value will be this amplitude multiplied by the length of the interval, if the length is long enough, any contributions due to the part of the solution near the origin will be washed out.

We are now ready to write the Parseval equation in the form

$$\begin{eqnarray*}\frac{m-m^*}{\lambda-\lambda*} & = & \sum_{i=0}^\infty\frac{r_i^2}{\vert\lambda - \lambda_i\vert^2} \end{eqnarray*}$$

which is valid for those values of m(b) which comply with all the requirements which we have set down, and the coefficients r_i, and the eigenvalues $\lambda_i$, are calculated with respect to a suitable Sturm-Liouville problem for each value of b.

The most effective technique which seems to have been found for passing to an infinite interval with the Parseval equality is to take it as an approximation to a Stieltjes integral

$$\begin{eqnarray*}\frac{m-m^*}{\lambda-\lambda*} & = & \int_{-\infty}^\infty\frac{d\rho(\mu)}{\vert\lambda-\mu\vert^2} \end{eqnarray*}$$

wherein the spectral distribution function $\rho(\mu)$ is approximated by a step function whose increment at the eigenvalue $\lambda_i$ is r_i². There are three logical possibilities at a point $\mu_0$ as the interval becomes infinite

1.

$\rho(\mu)$ has a discontinuity at $\mu_0$,

2.

$\rho(\mu)$ is continuous but not constant at $\mu_0$,

3.

$\rho(\mu)$ is continuous and constant at $\mu_0$

In the first case we say that $\mu_0$ is a point in the discrete spectrum of ${\cal L}$, in the second case we say that it is a point in the continuous spectrum of ${\cal L}$. $\mu_0$'s belonging to the third category are not spectral points. The classification agrees with the classification obtained from the resolvent in operator theory.

It cannot be emphasized too strongly that there are two aspects of the spectrum of the finite Sturm-Liouville problem which enter into the determination of $\rho$: one is the number of eigenvalues in any unit of interval, but the second is the value over the origin of the normalized eigenfunctions.

There is absolutely nothing in the theory which requires the spectral distribution function to be differentiable, yet it possesses this remarkable property in a majority of the examples of practical interest We could write, in such an event,

$$\begin{eqnarray*}\frac{m-m^*}{\lambda-\lambda*} & = & \int_{-\infty}^\infty\frac{\rho'd\mu}{\vert\lambda-\mu\vert^2} \end{eqnarray*}$$

and even

$$\begin{eqnarray*}{\rm Im}\ (m) & = & {\rm Im}\left\{\int_{-\infty}^\infty\frac{\rho'd\mu}{\lambda'-\mu}\right\}. \end{eqnarray*}$$

The derivative $\rho'$, when it exists, is called the spectral density function. A point to be borne in mind is that the m function is analytic in its domain of definition, and therefore might be expected to be differentiable. But remember that we are now talking about the boundary value, on the real axis, of a function which is not immediately defined there. It is therefore a matter of individual cases as to whether the real axis is a natural boundary, or whether the m function can be continued up to, and across, the real axis. We recall that this deficiency, of not being defined for real eigenvalues, which is shared by functions obtained from the bracket, was the motivation for working with a complex eigenvalue parameter at the outset.

If we have an analytic spectral distribution function, we are extremely fortunate, because it is possible to incorporate a great deal of complex analysis in the study of our differential operators. In particular, an analytic continuation of the spectral density may often be made across the real axis, into a region which is not accessible by the mere solution of a differential equation. In addition there are dispersion relations which can sometimes be written, which are very much related to questions of causality in some of the physical applications.

Since the spectral density is so closely related to the Weyl-Titchmarsh m function, the calculation of the latter can be used as a numerical technique for the location of the eigenvalues of a differential equation. Poles correspond to points in the discrete spectrum, whereas branch points delimit the intervals occupied by the continuous spectrum.

Traditional studies of the continuum have been noteworthy for their lack of imagination, taking it for granted that a continuum must be highly amorphous. For some potentials, notably the constant potential of a plane wave or even the Coulomb potential of the hydrogen atom, there is little which is remarkable about the spectral distribution function. Once the potential shows a little variability, however, it is found that the spectral density oscillates sedately, passing through a sequence of maxima and minima, whose sharpness and amplitude vary with the potential. Such oscillations imply possible poles in the m function the moment an analytic continuation is made across the real axis onto the unphysical sheet. In turn the poles encountered during the analytic continuation together with their residues may provide a very concise summary of the properties of the differential equation and its solutions, mathematically accessible through a Mittag-Leffler expansion of the m function.

It is not clear whether such a summary should be carried to the extent of attempting to construct an eigenfunction expansion based on the complex poles of the Titchmarsh-Weyl function. Most of the difficulty to be encountered in such an enterprise stems from the fact that an analytic continuation of the wave function is not necessarily a solution of the analytic continuation of its differential equation, or that it would be the same solution even if it satisfied the differential equation This discrepancy produces Stokes's phenomenon in the analytic continuation of a solution around a singular point of the coefficients of a differential equation. Indeed, the term ``unphysical sheet'' recognizes the fact that it contains functions which are not directly accessible as the solutions of Schrödinger's equation, but rather indirectly deduced through the process of continuation.

Sometimes it is possible to construct a biorthogonal set of functions employing the complex poles on the unphysical sheet, and sometimes it is possible to give a physical interpretation to the wave function on the physical sheet which is associated with one of the complex poles by ignoring the distinction between sheets. These associated wave functions tend to grow in the worst possible fashion, and so are possessed with an exponential growth which is too drastic to be accounted for by delta-function normalization. However, they do play a role in time-dependent problems, which gives an interpretation through the formation of wave packets, in which the real part of the pole signifies a resonance peak while the imaginary part is the reciprocal half-life for the decay of a transient state.

It is a mistake to treat the complex poles as energy levels, supposing that they are on the same footing as the poles on the real axis, which determine the bound states. Especially, they should be associated with wave functions with extreme caution. Still, when they are employed in a correct way the complex poles, together with branch points and other singularities, summarize the differential equation from which they arise, in the way that an analytic function is always determined by its singularities.