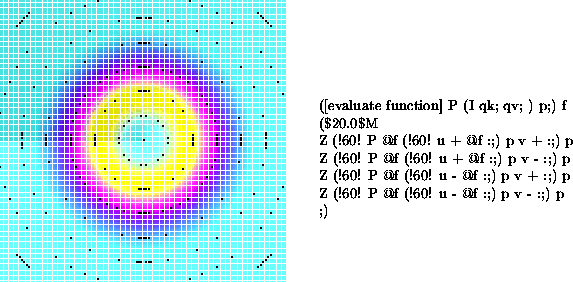representation by coloration

Color can be used to enhance drawings, but unless it is used with some discretion, the results can be totally confusing. One reason for this is that sharp boundaries are necessary for distinguishing objects, resulting in an amorphous appearance when viewing slowly graduated color schemes. Camouflaging makes good use of this circumstance. Some surface texture, such as inscribed contour lines, will greatly augment any use of color which may be present.

Nevertheless, scanning a region with the intention of placing colored pixels throught its interior can be performed easily, even when deducing contour lines would be quite a bit more complicated. One way to get a representation of complex numbers through a color code would be to use the color wheel which is thoroughly familiar in the television industry for the phase angle of the number. The grey scale would be entrusted to the modulus, running from white at zero to black at infinity, say.

Figure 13 shows an attempt at combining the two approaches, to put black pixels at integer moduli while color coding the rest of the plane. It is not entirely successful, mainly due to the interaction of pixel size with the criterion for integervaluedness.

  

Figure 13: Color coding of the plane according to the absolute value of each point. The black squares represent an attempt to distinguish contours at discrete heights.

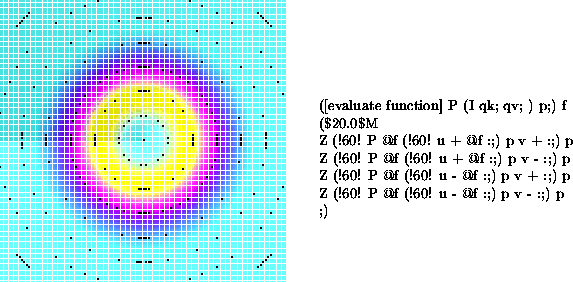It is probably much more understandable if the rainbow sequence is used to color code the modulus, ignoring the phase, or perhaps assigning it a slight grey scale. Of course, almost any system will highlight zeroes and poles, either because of color extremes or because they are enveloped by multiples of $2\pi$ radians with the attending color display. The problem lies in conveying a realistic appreciation for all the intervening values.

Because several coloring schemes are plausible, the operator for coloring little squares, qk, has been given a parameter, whose ASCII character values are assigned as follows:

l

- shading by logarithm of modulus, color by wheel

v

- color by hyperbolic tangent of modulus, shading by angle

a

- angle by color wheel, modulus by shading

r

- red

g

- green

b

- blue

c

- cyan

m

- magenta

y

- yellow

k

- black

o

- orange

v

- violet

Whatever the case, there is room to insert other alternatives in the list of parameter symbols, or to change the ones shown.

  

Figure 14: Color coded representation of the hyperbolic cosine (left) and the hyperbolic tangent (right).

Figure 14 shows two common functions of a complex variable, the hyperbolic cosine and the hyperbolic tangent. Of coures, they become the ordinary cosine and tangent after rotation by $90^\circ$ and show the periodicity of these functions along the imaginary axis.