A Case Study: the cis-Ternary Pentagonal Flexagon

Ternary flexagons are those whose map has three cycles. For symmetry reasons when using regular pentagons, there are only two ternary flexagons, which can be called cis-ternary and trans-ternary from the viewpoint of chemical nomenclature. In the cis- form, the two secondary rings are adjacent; in the trans- form, they are separated.

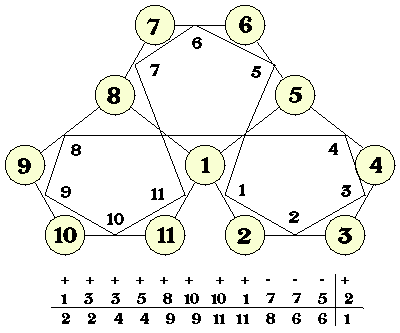
To get the plan of a flexagon, its map is first drawn, and the Tukey Triangle network set up; it may be more appropriate to call them Tukey pentagons in this case. The result is shown in Figure 8, below.

  

Figure 8: Map, with Tukey pentagons, of the cis-ternary pentagonal flexagon.

The essential element of Figure 8 is the sign sequence which describes the succession of edge reflections used to make the plan. They must be translated into REC in terms of N's and n's. In order to have the longest runs of like signs, the map was numbered in just the way shown in the figure, producing the sign sequence {+ + + + + + + + - - - }.

Using X5 to create the original pentagon,

(X5 CN CN CN CN CN CN CN CN Cn Cn Cn ;),

would give a satisfactory plan, each N corresponding to a + and each n to a -. The resulting plan has a kink, with some of the pentagons overlapping others. Such conflicts can be resolved one way or another. Since preserving the hinging edges is what really matters, overlapping polygons can be cut apart and the resulting fragments used even when they are in tatters.

If that is impractical, or it is desired to preserve the full polygon, the plan can be interrupted and the continuation offset, by using the REC operator o, sometimes several times to get a good separation.

Using a counter to avoid repeating CN over and over (there is a crossover point before which repetition is shorter than counting), the program which is finally used is

([cis-ternary pentagonal] X5 N P (!8!CN :;)PCoo p (!4! Cn:;) p;).

Actually, an extra count is given for each stretch, together with the push and pop operators. The reason is to have an extra polygon which can be glued to its equivalent in the next stretch to join the pieces together. Having repeated the bridging polygon, the program returns to where it left off before continuing. The exterior push-pop pair is actually unnecessary, but is useful in a library where one strip needs to be inserted into another without losing continuity.

  

Figure 9: Panels used in drawing the cis-ternary pentagonal flexagon. The right panel is just the text field from the main window in ``external'' mode.

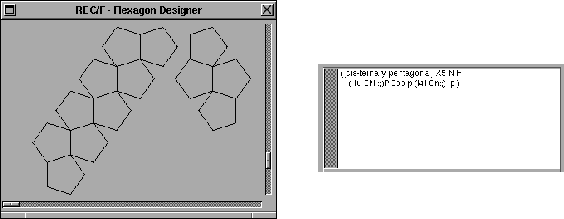Once a satisfactory plan has been created, it can be transferred to the Draw program for lettering and coloring.

  

Figure 10: The cutout page from which the final flexagon may be cut, folded and pasted. Left: the top side. Right: the bottom side. Not all the pentagons have been colored; only those which are faces appearing in two different cycles. If they are visible while flexing the flexagon, the mountain-valley transition will switch cycles.

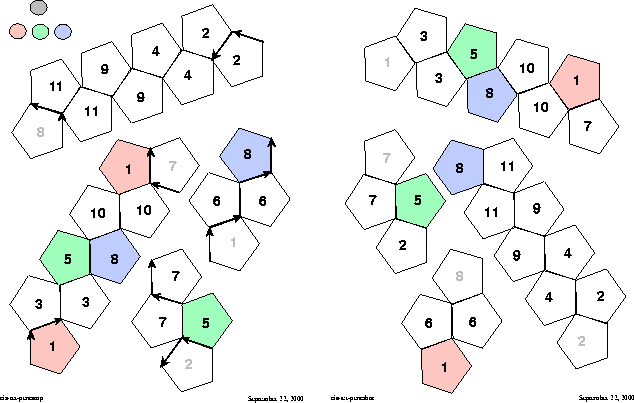In this case, the plan is of odd length, so it is convenient to show the second upside down plan on the same page; in any event the pentagons are going to be rather small, and will be no smaller on account of this accomodation. Top and Bottom pages will have to be prepared anyway; one of the inconveniences of Draw is that it does not reflect images, maybe to avoid trying to reflect lettering.