Some applications of REC-R

Coefficient matrices from Equation 1 are defined in sero.c which is a part of SERO, according to the following extract:

/*  [Pot. 1: Onda plana, ec. de Schroedinger] */
void potl1(u,e,z) double *u, e, z; {
u[0]=0.0; u[1]=-2.0*e; u[2]=1.0; u[3]=0.0;}

/*  [Pot. 2: Pozo finito, ec. de Schroedinger] */
void potl2(u,e,z) double *u, e, z; {double h, q;
h=0.5*wi; q=(z<-h||z>h)?0.0:-hi;
u[0]=0.0; u[1]=q-2.0*e; u[2]=1.0; u[3]=0.0;}

/*  [Pot. 3: Barrera finita, ec de Schroedinger] */
void potl3(u,e,z) double *u, e, z; {double h, q;
h=0.5*wi; q=(z<-h||z>h)?0.0:hi;
u[0]=0.0; u[1]=q-2.0*e; u[2]=1.0; u[3]=0.0;}

/*  [Pot. 4: Escalon, ec. de Schroedinger] */
void potl4(u,e,z) double *u, e, z; {
u[0]=0.0; u[1]=((z>=0.0)?st:0.0)-2.0*e; u[2]=1.0; u[3]=0.0;}

/*  [Pot. 5: Oscilador armonico, ec. de Schroedinger] */
void potl5(u,e,z) double *u, e, z; {
u[0]=0.0; u[1]=z*z-2.0*e; u[2]=1.0; u[3]=0.0;}

/*  [Pot. 6: Oscilador cuartico, ec. de Schroedinger] */
void potl6(u,e,z) double *u, e, z; {double x;
u[0]=0.0; x=z*z; u[1] = 0.1*x*x -x -2.0*e; u[2]=1.0; u[3]=0.0;}

/*  [Pot. 7: Oscilador armonico factorizado, ec. de Dirac] */
void potl7(a,e,z) double *a, e, z; {double s, t, u, v;
s=0.1667*z*z-e; t=2.0*s*z; u=em*sin(t); v=em*cos(t);
a[0]=-u; a[1]=v; a[2]=v; a[3]=u;}

/*  [Pot. 8: Gaussian Potential, ec. de Dirac] */
void potl8(u,e,z) double *u, e, z; {double g;
g=st*exp(-(z*z)/wi); u[0]=0.0;
 u[1]=em+g-e; u[2]=em-g+e; u[3]=0.0;}

/*  [Pot. 9: Sinusoidal potential] */
void potl9(u,e,z) double *u, e, z; {
u[0]=0.0; u[1]=hi*cos(z)-2.0*e; u[2]=1.0; u[3]=0.0;}

/*  [Pot. 10: Linear potential] */
void potl10(u,e,z) double *u, e, z; {
u[0]=0.0; u[1]=-z-2.0*e; u[2]=1.0; u[3]=0.0;}

/*  [Pot. 11: Coulomb potential] */
void potl11(u,e,z) double *u, e, z; {
u[0]=0.0; u[1]=(z>-7.4?-1.0/(z+7.5):0.0)-1.0*e;
 u[2]=1.0; u[3]=0.0;}

/*  [Pot. 12: Inverse Square potential] */
void potl12(u,e,z) double *u, e, z; {
u[0]=0.0; u[1]=((z>=-7.5)?-25.0/((z+7.6)*(z+7.6)):0.0)-1.0*e;
u[2]=1.0; u[3]=0.0;}

/*  [Pot. 13: Damped classical oscillator with forcing] */
void potl13(u,e,t) double *u, e, t; {double g;
u[0]=-0.1; u[1]=-2.0*e; u[2]=1.0; u[3]=0.0;
g=0.2*sin(3.0*t); u[4]=u[5]=g; u[6]=u[7]=0.0;}

/*  [Pot. 14: Dirac Harmonic Oacillator] */
void potl14(u,e,z) double *u, e, z; {double g;
g=0.1666*z*z; u[0]=0.0; u[1]=em+g-e; u[2]=em-g+e; u[3]=0.0;}

/*  [Pot. 15: Factored Inverse Square] */
void potl15(u,e,z) double *u, e, z; {double s, c, g, qq;
qq=0.2*(z+7.6); g=log(0.2*(z+7.6)); s=sin(g); c=cos(g);
u[0]=-(e*c*s*qq); u[1]=-(e*c*c*qq); u[2]=e*s*s; u[3]=e*s*c;}

/*  [Pot. 18: Dirac Sinusoidal potential] */
void potl18(u,e,z) double *u, e, z; {double p; 
switch(0) {
case 0:  p=hi*cos(z); break;
case 1:  p=hi*(cos(z)-0.333*cos(3.0*z)); break; /* flat    */
case 2:  p=hi*(cos(z)+0.333*cos(3.0*z)); break; /* sharp   */
case 3:  p=hi*(cos(z)-0.333*cos(3.0*z)+0.2*cos(5.0*z)); 
                                         break; /* flatter */
case 4:  p=0.67*hi*(cos(z)+0.333*cos(3.0*z)+0.2*cos(5.0*z));
                                         break; /* sharper */
case 5:  p=0.2*hi*(cos(z)+cos(2.0*z)+cos(3.0*z))+
                  cos(4.0*z)+cos(5.0*z); break; /* deltoid */
default: p=hi*cos(z); break;
}
u[0]=0.0; u[1]=em+p-e; u[2]=em-p+e; u[3]=0.0;}

/*  [Pot. 19: Quarkish Harmonic Oscillator] */
void potl19(u,e,z) double *u, e, z; {
u[0]=hi*z; u[1]=em-e; u[2]=em+e; u[3]=-hi*z;}

The results would be much more attractive if they were displayed in a table rather than just as C subroutines; some of them are shown below.

$$% latex2html id marker 464 \begin{array}{ccc} {\rm index} &... ...y} \right] & {\rm VJ:\ quarkish\ oscillator} \\ \end{array}$$

The first example, shown in Figure 9, solves no differential equation, but it illustrates the machinery for which REC is considered as a useful interface to some other program. Of course, even such a small example is still too complicated to be typed casually at the console, but its program-like structure incorporates many choices and initializations that would be harder to accomodate in the graphical user interface style.

The inner loop, whose purpose is to run out a single graph whose parameters remain constant, consists of the REC expression (!90! s pc g : ;) whose counter calls for 90 points on the graph. The graphic variable s is autoincrementing and goes onto the pushdown list first as the x-coordinate.

Since it autoincrements, it cannot be used a second time to get the y-coordinate, but its value can be duplicated by pushing, vololowing which it is clipped by a hyperbolic tangent which leaves a fairly true interval -1 < y < 1, but quickly flattens the variable elsewhere.

The next outward loop has charge of drawing a family of coves, in this case 20. It is the place where a parameter governing the curve could be varied, but that is missing in this example. But the tail of the loop does contain the operator a, responsible for the increasing offset as each curve is drawn. Correspondingly, the head of this loop initializes the x coordinate anew (and independently of the action of the offset, which is only applied as the graph is being drawn).This is done by the sequence -5.0 n 0.1 n S which feeds the origin -5.0 and increment 0.1 to the initializing operator S.

  

Figure 9: A rudimentary REC-R program which only graphs a constant, but clipped, straight line. It illustrates the initialization of the graphing variable, the application of offsets to successive graphs, and the advantages of clipping, to keep the entire body of the graph within the graphing area. Hidden line suppression would not alter this graph, but there is a noticable jump where the first value has not been chosen carefully. Sometimes this ``bug'' is a ``feature'' as when it shows a zero-point.

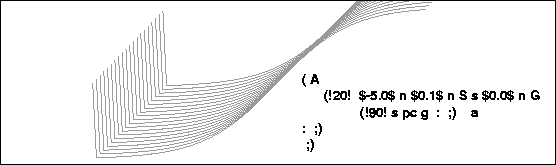The choice of these numbers is governed by the fact that the screen is comparable in size to a sheet of paper, so that ten inches measures the extent of the graphing area, in which the pixels are maybe hundredths of an inch, so ten pixels, or a tenth of an inch, is a good increment. Actually, PostScript uses points, and actually, SERO scales everything anyway, so the numbers cited are the ones to think about when planning the dimensions of graphs.

The initial point for graph movements is established by s 0.0 n G, which shows why all the curves drop down to zero at the left. That is deliberate, but it could be avoided by writing s p G instead.

Finally, the offset operating in the middle loop has to be initialized in the outer program by the operator A.

Going on to a more complicated example with a potential and for which the graphing is driven by the Runge-Kutta variable, Figure 10 shows the solution at a single energy for potential number 5, the Schrödinger harmonic oscillator.

This time there is a preface V5 [Harmonic oscillator] 7.5 E 0.05 D which selects the potential, sets the energy level, and selects a Runge-Kutta step size, which is half the default. It is followed by the first inner loop, which initializes the differential equation, sets up the first point in the graph, and then runs out 200 points and graphs them, namely u 0.0 o v i c G (!200! r v i c g : ;) .

The operator i means that the derivative of the odd solution, which is even, is being graphed. To get the solution itself, j should have been chosen. There is no reason they could not both have been graphed in the same box, if the additional code had been included. That is far preferable to trying to graph both solutions at once out of the same matrix, but for more extensive calculations it would have to be a trade-off between the costs of Runge-Kutta steps and pen movements.

  

Figure 10: Another rudimentary REC-R program which graphs a single wave function at one energy of the Schrödinger harmonic oscillator. Outside the potential well the function is exponential, but it has been clipped for aesthetic reasons, namely keeping the graph within a bounding box.

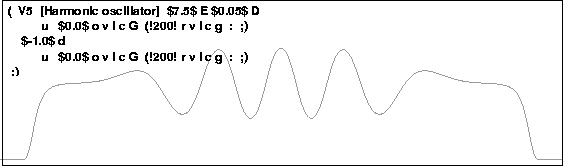The line between the two inner loops reverses the direction of the Runge-Kutta step.

  

Figure 11: A more ambitious version of the program which graphs a single wave function shows twenty wave functions at small increments, crossing the value at which the asymptotic wave function changes sign.

In Figure 11 a second loop has been added which varies the energy eigenvalue. The result is graphed plain, without the suppression of hidden lines because the result is still intelligible, and in fact, slightly preferable in that form. The interesting aspect of the graph is that the energy crosses the value at which the sign of the asymptotic exponential changes. Assuming, by continuity, that there is an energy at which the asymptotic value is zero, one has found one of the quantized energy levels.

Because subroutines are used in the program of Figure 11, they are named and enclosed along with the main program between a pair of braces. There is no way for a main program to call itself, although that is a recursive possibility. Should such a thing be required, it is easy enough to assign the main program some name, create a new main program whose only content is to call the old main program, and procede as though nothing had happened. Who is it that once said that it is a poor program which does not even know its own name?

Figure 12 shows a more elaborate construction, in which the predicate sensing the difference between the classically accessible region and the classically forbidden region has been used to color the two parts of the graph differently.

It is a commentary on the mechanism maintaining the horizons that this figure cannot be rendered with hidden lines suppressed. The reason is that drawing the two halves of each curve separately, outwards from the center, runs counter to the indexing scheme for the horizon. This is a blemish which could, of course, be fixed.

  

Figure 12: A more ambitios version of the program which graphs a single wave function shows twenty wave functions at small increments, crossing the value at which the asymptotic wave function changes sign.

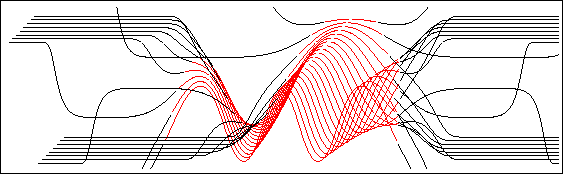The program which drew Figure 12 is the following:

{
([ put 150 increments per trajectory] !150! ;) n 
([ solution 10 in classical region]  Cr  v l c  G  (r  F;  @n v l c g : ); ) i 
([ solution 10 in forbidden region]  Ck v l c  G  (r  (F); @n v l c g : ); ) I 
([ get the solution in one direction]  u $0.0$ o  (r  @i @I: ;) ;) h  
    (  A V5  [Harmonic oscillator]   $5.0$ E $0.05$ D $-1.0$ U 
       (!20!  (@n:;)  @h   $-1.0$ d   (@n:;)  @h  $-0.25$ e a: ;)   ;)
}

The counter @n has been set aside as a subroutine to maintain the continuity of counting in either of the two regions of the graph, however they alternate. Placing a counter in a subroutine is a standard technique to access the same count from different parts of a program; of course it must be initialized, as is done in (@n:;), by exausting the count whenever it needs to be reset.

There are two predicates in REC-R which can be used for coloring surfaces, b which tests the sign of the variable on the pushdown list, and B which tests whether the variable lies in the range -1 < y < 1. The latter is mostly used in judging whether angles of rotation are real or imaginary, often used in constructing stability charts for periodic equations.

Although REC-R has a pushdown list, there is no provision for using it like a hand-held calculator. Some future version may consider the extension useful, at the very least for forming linear combinations of matrix alememnts or of solution vectors.

The examples which have been shown up to now utilize the fixed rectangular ``solution window'' in REC-R. To use this window, which is always centered on zero, it is convenient to keep in mind that $\pm 10.0$ is the range of the independent variable and $\pm 2.0$ of the dependent variable, more or less. A reference line representing the x-axis could be generated by the REC sequence ([reference axis] A $-7.5$ n $0.0$ n G $7.7$ n $0.0$ n g;), but any other line could be made by choosing suitable coordinates.

The other window, the ``phase window,'' follows the same scaling, but its overall size and shape are adjustable by the sizing bar on its bottom margin. To use this window, it is only necessary to press the corresponding button and, of course, to have chosen a suitable pair of variables for the coordinates.

  

Figure 13: A few phase plane trajectories, with offsets, are graphed to compare their behavior near a resonance.

Figure 13 exhibits such a window with the harmonic oscillator phase plane. The corresponding code, which uses j and l to summon the coordinates rather than l and v, is:

{ ([ put 100 increments per trajectory] !100! ;) n 
([ solution 10 in classical region] Cr j c l c  G (r  F;  @n j c l c g : ); ) i 
([ solution 10 in forbidden region] Ck j c l c  G (r (F); @n j c l c g : ); ) I 
([get the solution in one direction]  u $0.0$ o  (r  @i @I: ;) ;) h  
    ( A V5  [Harmonic oscillator]   $3.0$ E $0.05$ D $-0.75$ U 
      (!4!  (@n:;)  @h  $-1.0$ d  (@n:;)  @h  $0.4255$ e a: ;) ;) }

Of course, neither window has an exclusive use, and having two is probably redundant. When a large graph is desired, consisting of a large number of offset images, the phase window is especially convenient.