



Next: Subrutina CNTU
Up: Subrutinas que usa el
Previous: Subrutina RUKU
Contents
Ya se discutió en otro lado de dónde surge el concepto de
puntos de retorno y se encontró que existen dos potenciales
efectivos, uno en  y otro en
y otro en  . Dichos potenciales
venían expresados como polinomios de cuarto grado, ecuaciones
(I-5-1).
Se ha construido un programa para graficar dichos polinomios, se
trata de la subrutina TURN que vamos a discutir ahora. Tal
vez sería más conveniente elaborar una subrutina que
evalúe las raíces de los polinomios a que nos estamos
refiriendo, dichas raíces corresponderían a los puntos
clásicos de retorno pero se optó mejor por construir
gráficas. El listado de TURN es el siguiente:
. Dichos potenciales
venían expresados como polinomios de cuarto grado, ecuaciones
(I-5-1).
Se ha construido un programa para graficar dichos polinomios, se
trata de la subrutina TURN que vamos a discutir ahora. Tal
vez sería más conveniente elaborar una subrutina que
evalúe las raíces de los polinomios a que nos estamos
refiriendo, dichas raíces corresponderían a los puntos
clásicos de retorno pero se optó mejor por construir
gráficas. El listado de TURN es el siguiente:
SUBROUTINE TURN (H,ALFA,PPHI,EPP,EPM,GPL,GMI,XK)
DIMENSION A(5),B(5),III(100)
A(1)=H
A(2)=-EPP
A(3)=-(ALFA+H+GMI*GMI)
A(4)=EPP-2.0*PPHI*GMI
A(5)=ALFA-PPHI*PPHI
B(1)=H
B(2)=-EPM
B(3)=-(ALFA+H+GPL*GPL-XK)
B(4)=EPM-2.0*PPHI*GPL
B(5)=ALFA-PPHI*PPHI-XK
WRITE (3,350) A
350 FORMAT ('COEFICIENTES EN PXI (+) ARE ',5F10.4)
WRITE (3,351) B
351 FORMAT (' COEFICIENTE EN PETA (*) ARE ',5F10.4)
WRITE (3,352) H,ALFA,PPHI
352 FORMAT (' H= ',F10.4,',ALFA = ',F10.4,', PPHI = ',F10.4)
X=-1.0
DO 20 J=1,50
DO 2 I=1,100
2 III(I)=1H
III(50)=1HI
Z=A(1)
DO 4 I=2,5
4 Z=Z*X+A(I)
W=B(1)
DO 6 I=2,5
6 W=W*X+B(I)
IW=5.0*W/ABS(H)+50
IZ=5.0*Z/ABS(H)+50
IF (IZ) 30,30,31
30 IZ=1
31 IF (IW) 32,32,33
32 IW=1
33 IF (100-IZ) 34, 35,35
34 IZ=100
35 IF (100-IW) 36,37,37
36 IW=100
37 CONTINUE
III(IZ)=1H+
III(W)=1H*
WRITE (3,300) X,Z,W,III
300 FORMAT (1X,F6.2,2F7.2,100A1)
X=X+O.1
20 CONTINUE
WRITE (3,301)
301 FORMAT (1H1)
RETURN
END
Los argumentos de la subrutina son:
H, ALFA, PFI, EPM, GPL, GMI Y XK
que corresponden a las constantes que componen los
coeficientes de polinomios. Dichos polinomios tienen la forma
que como hemos visto, corresponden a las ecuaciones (I-5-1).
Dichos coeficientes se van a guardar en dos arreglos de cinco
elementos cada uno como sigue:
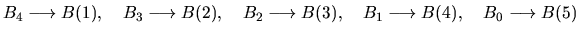 .
En la misma forma se procede con el arreglo A. La forma de
dichos coeficientes puede verse en las ecuaciones (I-5-1) y van a
permanecer constantes durante todo el cálculo.
Antes de graficar se imprimen algunas constantes de interés como
puede verse en los ejemplos.
Se tiene presente el rango de validéz que tiene
.
En la misma forma se procede con el arreglo A. La forma de
dichos coeficientes puede verse en las ecuaciones (I-5-1) y van a
permanecer constantes durante todo el cálculo.
Antes de graficar se imprimen algunas constantes de interés como
puede verse en los ejemplos.
Se tiene presente el rango de validéz que tiene  que en este
programa representamos por la varible X.
La técnica de graficación es la misma que ya se explicó por
lo que no tiene caso explicarla aquí. Lo que si es importante
señalar aquí, es que desde el punto de vista computacional,
la manera más adecuada de escribir un polinomio es la siguiente:
que en este
programa representamos por la varible X.
La técnica de graficación es la misma que ya se explicó por
lo que no tiene caso explicarla aquí. Lo que si es importante
señalar aquí, es que desde el punto de vista computacional,
la manera más adecuada de escribir un polinomio es la siguiente:
y para calcular, usamos una variable 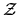 que va cambiando
sucesivamente su valor partiendo desde el paréntesis más
interno hasta tener calculado todo el polinomio. Esa manera de
hacer el cálculo reduce al mínimo el número de
operaciones.
Como la función toma valores positivos y negativos, se escribe el
eje en la mitad del arreglo. Además se va a utilizar una escala
de 1:5 ( factor de IW o IZ) lo que nos indica que
tendremos 5 unidades por columna. Además como los valores de
que va cambiando
sucesivamente su valor partiendo desde el paréntesis más
interno hasta tener calculado todo el polinomio. Esa manera de
hacer el cálculo reduce al mínimo el número de
operaciones.
Como la función toma valores positivos y negativos, se escribe el
eje en la mitad del arreglo. Además se va a utilizar una escala
de 1:5 ( factor de IW o IZ) lo que nos indica que
tendremos 5 unidades por columna. Además como los valores de
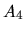 y
y 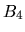 son dados por H, la escala es dependiente de
la energía si no dividimos toda la función por H. Al
calcular
son dados por H, la escala es dependiente de
la energía si no dividimos toda la función por H. Al
calcular 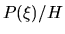 se toma el valor absoluto de H porque
nos interesa conservar el signo de la función; ya hemos visto
que los ceros de un polinomio no cambian si lo multiplicamos o
dividimos por una constante; así es que no hemos hecho nada
malo.
Al igual que en otras gráficas, se procura que la curva permanezca
siempre en el intervalo de graficación.
se toma el valor absoluto de H porque
nos interesa conservar el signo de la función; ya hemos visto
que los ceros de un polinomio no cambian si lo multiplicamos o
dividimos por una constante; así es que no hemos hecho nada
malo.
Al igual que en otras gráficas, se procura que la curva permanezca
siempre en el intervalo de graficación.




Next: Subrutina CNTU
Up: Subrutinas que usa el
Previous: Subrutina RUKU
Contents
Pedro Hernandez
2006-02-20