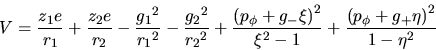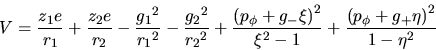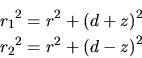Next: Subrutina PRYPO
Up: Subrutinas que usa el
Previous: Subrutina TURN
Contents
Con la subrutina CNTU se grafica la región donde puede
moverse la partícula. Pueden también graficarse los niveles de
energía potencial constante; esto se consigue sombreando las
regiones donde la energía está comprendida dentro de ciertos
rangos de valores y lo que se va a observar son franjas sombreadas y
sin sombrear alternadas y los contornos de tales franjas
corresponderán a diferentes niveles de energía potencial siendo
constante la diferencia entre niveles sucesivos. La expresión del
potencial que usaremos para nuestro programa es el potencial efectivo
dado por:
Pueden hacerse todas las modificaciones necesarias tales como
eliminar los términos correspondientes al potencial repulsivo o
solo considerar esos términos, etc. Se usará una hoja completa
para esta gráfica, es decir, se tendrán cincuenta renglones de
ciento veinte columnas.
SUBROUTINE CNTU (G1,G2,Z1,Z2)
DIMENSION III (120)
DO 10 I=1,50
DO 2 J=1,120
2 III(J)=16448
Y=(50-I)*0.082
DO 11 J=1,120
X=J*0.05-3.0
S1=(X+1.0)**2+Y*Y
S2=(X-1.0)**2+Y*Y
U=(G1*G1)/S1+(G2*G2)/S2+Z1/SQRT(S1)+Z2/SQRT(S2)
U=10.0*U
IF (U-10.0) 20,20,43
20 IF (U+10.0) 41,21,21
21 IF (U) 30,30,33
30 IF (U+0.5) 31,31,41
31 IF (U+1.0) 32,32,11
32 U=U+1.
GO TO 32
33 IF (U-0.5) 11,11,34
34 IF (U-1.0) 43,43,35
35 U=U-1.0
GO TO 33
41 III (J)=24640
GO TO 11
43 III(J)=20032
11 CONTUNUE
WRITE (3,320) III
320 FORMAT (1X,120A1)
10 CONTINUE
WRITE (3,321)
321 FORMAT (1H1)
RETURN
END
La técnica empleada es muy burda: Sobre la línea 50 se
escribirá el eje Z y sobre el eje vertical representaremos al
radio cilíndrico tomando en cuenta que:
como puede apreciarse en la Figura 3.2.
Figure 3.2:
coordenadas
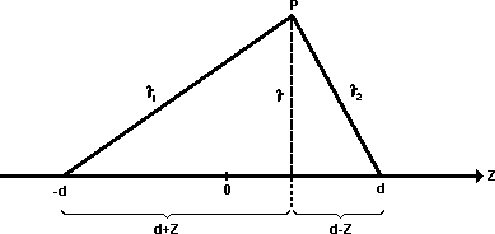 |
Las posiciones -1 y 1 en las que se han colocado los dos centros
corresponden en nuestra gráfica a las columnas 40 y 80
respectivamente.
Al mapear R contra Z resultarán figuras de
revolución alrededor de este último eje. Como todo estará en
función de Z, entonces se calculará dicha variable en
todo punto de la gráfica. Lo mismo que en programas que hemos
discutido antes, aquí también se hacen los ajustes de
escala adecuados, a los renglones se les representa como Y
que en nuestro caso corresponden a r, se les da el valor
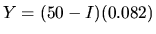 , ya que tomaremos el cero en el renglón 50. Se
ha convenido en dar a la columna 80 el valor 1, y entonces, la
columna 120 valdrá 3; por lo que a las columnas las
representaremos como
, ya que tomaremos el cero en el renglón 50. Se
ha convenido en dar a la columna 80 el valor 1, y entonces, la
columna 120 valdrá 3; por lo que a las columnas las
representaremos como
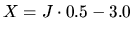 ; de acuerdo con eso el
potencial, al que representamos por U, será del tipo
U(X,Y) pudiendo tomar valores positivos tanto como negativos.
Hemos discutido ya los detalles del programa que merecen
discusión, el resto no difiere esencialmente de lo que se ha
visto en otras gráficas.
; de acuerdo con eso el
potencial, al que representamos por U, será del tipo
U(X,Y) pudiendo tomar valores positivos tanto como negativos.
Hemos discutido ya los detalles del programa que merecen
discusión, el resto no difiere esencialmente de lo que se ha
visto en otras gráficas.




Next: Subrutina PRYPO
Up: Subrutinas que usa el
Previous: Subrutina TURN
Contents
Pedro Hernandez
2006-02-20