



Next: Discusión del programa PRYPO
Up: F A C U
Previous: Estudio del movimiento considerando
Contents
En esta tesis se logró separar variables recurriendo a un
artificio matemático que consiste en sumar a la función
Hamiltoniana un potencial repulsivo de la forma 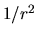 . En
principio el problema queda resuelto y puede hacerse un estudio
sobre las órbitas en términos de variables de acción y
ángulo; sin embargo, es necesario utilizar integrales
elípticas para las que es preciso factorizar un polinomio de
cuarto grado y ya se discutió qué dificultades presenta su
tratamiento. Como consecuencia de éso, un estudio del movimiento
en los términos que se hizo aquí, presenta algunas
limitaciones. Además, el hecho de mantener fija la distancia
entre los dos centros no permite reducir el problema a casos
semejantes a los efectos Stark, Zeeman, etc., los cuales pueden
resultar más simples.
Respecto a la parte numérica, debemos hacer la observación que
en todos los ejemplos que obtuvimos se utilizaron diferentes
valores para el incremento durante la integración numérica y
no hubo nunca una diferencia notable en los resultados, por lo que
no tuvimos problemas con la estabilidad, eso, por supuesto no
significa que no sea necesario un estudio más a fondo sobre las
ecuaciones diferenciales, no se hizo ningún estudio acerca de la
estabilidad en las ecuaciones diferenciales. Esto es importante
porque en todos los problemas. resueltos numéricamente va
implícito un error de truncamiento, la computadora introduce
al mismo tiempo un error de redondeo en los cálculos. Sin
embargo, eso no fue el propósito de nuestra tesis, aunque en un
estudio más completo no pueden omitirse esos detalles.
En la referencia número 21 se hacen consideraciones acerca de
cuáles son los incrementos óptimos en cada punto, tomando como
criterio la curvatura de las trayectorias. A pesar de lo que hemos
dicho, pueden estudiarse varias posibilidades de las que ya se habló
a lo largo de la exposición; por ejemplo, el problema de Kepler,
combinaciones de cargas eléctricas y magnéticas en un centro, etc.
La parte que nos da mayor información es el estudio de las
funciones
. En
principio el problema queda resuelto y puede hacerse un estudio
sobre las órbitas en términos de variables de acción y
ángulo; sin embargo, es necesario utilizar integrales
elípticas para las que es preciso factorizar un polinomio de
cuarto grado y ya se discutió qué dificultades presenta su
tratamiento. Como consecuencia de éso, un estudio del movimiento
en los términos que se hizo aquí, presenta algunas
limitaciones. Además, el hecho de mantener fija la distancia
entre los dos centros no permite reducir el problema a casos
semejantes a los efectos Stark, Zeeman, etc., los cuales pueden
resultar más simples.
Respecto a la parte numérica, debemos hacer la observación que
en todos los ejemplos que obtuvimos se utilizaron diferentes
valores para el incremento durante la integración numérica y
no hubo nunca una diferencia notable en los resultados, por lo que
no tuvimos problemas con la estabilidad, eso, por supuesto no
significa que no sea necesario un estudio más a fondo sobre las
ecuaciones diferenciales, no se hizo ningún estudio acerca de la
estabilidad en las ecuaciones diferenciales. Esto es importante
porque en todos los problemas. resueltos numéricamente va
implícito un error de truncamiento, la computadora introduce
al mismo tiempo un error de redondeo en los cálculos. Sin
embargo, eso no fue el propósito de nuestra tesis, aunque en un
estudio más completo no pueden omitirse esos detalles.
En la referencia número 21 se hacen consideraciones acerca de
cuáles son los incrementos óptimos en cada punto, tomando como
criterio la curvatura de las trayectorias. A pesar de lo que hemos
dicho, pueden estudiarse varias posibilidades de las que ya se habló
a lo largo de la exposición; por ejemplo, el problema de Kepler,
combinaciones de cargas eléctricas y magnéticas en un centro, etc.
La parte que nos da mayor información es el estudio de las
funciones 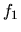 ,
, 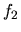 ,
, 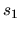 y
y 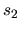 , definidas en la sección
I.5.1, y sobre las que se insistió bastante a lo largo de la
exposición. El estudio de sus gráficas tiene la ventaja de que
permite formarse una idea cualitativa acerca de la importancia de
cada uno de los parámetros en el movimiento.
Aunque la separación de variables no es posible cuando se excluye
el potencial repulsivo, existe la posibilidad de obtener diferentes
trayectorias utilizando los mismos métodos numéricos que se
emplearon en el presente trabajo. De hecho, hemos incluído un
apéndice donde se modifican los programas para considerar dicha
posibilidad.
Por otra parte, una de nuestras preocupaciones ha sido la de
presentar el material de tal manera que pueda servir como ilustración
de cómo atacar problemas en mecánica Hamiltoniana, utilizando como
herramienta importante las computadoras.
Se espera que sea de utilidad.
, definidas en la sección
I.5.1, y sobre las que se insistió bastante a lo largo de la
exposición. El estudio de sus gráficas tiene la ventaja de que
permite formarse una idea cualitativa acerca de la importancia de
cada uno de los parámetros en el movimiento.
Aunque la separación de variables no es posible cuando se excluye
el potencial repulsivo, existe la posibilidad de obtener diferentes
trayectorias utilizando los mismos métodos numéricos que se
emplearon en el presente trabajo. De hecho, hemos incluído un
apéndice donde se modifican los programas para considerar dicha
posibilidad.
Por otra parte, una de nuestras preocupaciones ha sido la de
presentar el material de tal manera que pueda servir como ilustración
de cómo atacar problemas en mecánica Hamiltoniana, utilizando como
herramienta importante las computadoras.
Se espera que sea de utilidad.




Next: Discusión del programa PRYPO
Up: F A C U
Previous: Estudio del movimiento considerando
Contents
Pedro Hernandez
2006-02-20