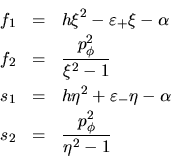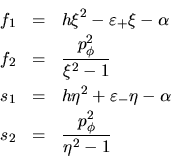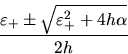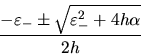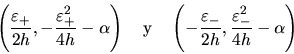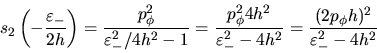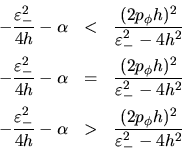Next: Conclusiones.
Up: Algunos ejemplos de configuraciones
Previous: Energías negativas
Contents
Ya vimos lo que ocurre cuando se consideran cargas magnéticas
únicamente, ahora vamos a ver el movimiento cuando existen solamente
cargas eléctricas en nuestro problema. La forma de nuestras funciones
será la misma, pero ahora los términos que contienen factores
de  y
y  son cero, tendremos por consiguiente
son cero, tendremos por consiguiente
Como no hay términos de origen magnético las curvas
correspondientes a 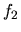 y
y 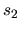 serán exactamente iguales y
además se tendrá simetría completa por tener sólo
términos cuadráticos en sus variables correspondientes. Lo que
hay que hacer en cada caso es un estudio de las raíces dentro
de los rangos en que cada variable tiene significado físico,
como lo hemos venido haciendo en otros casos.
Ahora, el parámetro
serán exactamente iguales y
además se tendrá simetría completa por tener sólo
términos cuadráticos en sus variables correspondientes. Lo que
hay que hacer en cada caso es un estudio de las raíces dentro
de los rangos en que cada variable tiene significado físico,
como lo hemos venido haciendo en otros casos.
Ahora, el parámetro 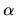 nos da las intersecciones con el eje
vertical de las parábolas
nos da las intersecciones con el eje
vertical de las parábolas 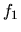 y
y 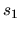 con el eje vertical, aunque
ambas familias no son idénticas por la presencia de los parámetros
con el eje vertical, aunque
ambas familias no son idénticas por la presencia de los parámetros
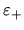 y
y 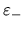 .
Las intersecciones de
.
Las intersecciones de 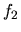 y
y 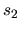 con el eje horizontal vendrán
dadas por
con el eje horizontal vendrán
dadas por
y por
respectivamente y la posición de los vértices será en cada
caso
En este caso nos damos cuenta rápidamente que los estados ligados
corresponden siempre a energías negativas, además para tener
soluciones con significaso físico en -- debemos tener que --
debe ser negativa, otra cosa que debemos pedir para esta variable es
que la pendiente de la energía cero debe ser positiva, es decir
o sea
Eso implica que al menos uno de los dos centros debe ser atractivo y
además predominante; si los dos centros son atractivos la desigualdad
anterior se cumple siempre y entonces hay problema, no importará
mucho que valores tengamos para 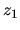 y
y 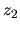 .
Por lo que respecta a las curvas para
.
Por lo que respecta a las curvas para  sólo nos interesan
intersecciones que esten dentro del rango
sólo nos interesan
intersecciones que esten dentro del rango 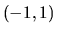 y serán
posibles las siguientes configuraciones Figura 4.3.
y serán
posibles las siguientes configuraciones Figura 4.3.
Figure 4.3:
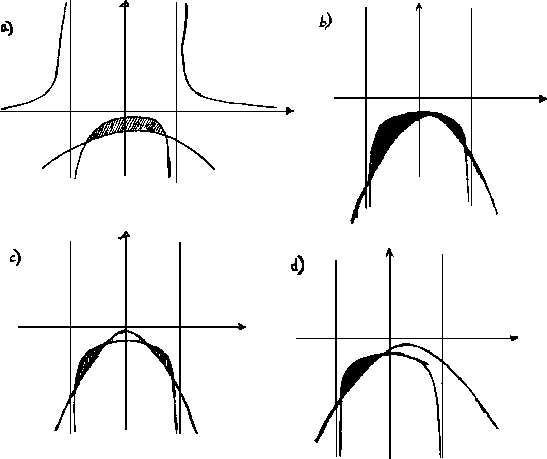 |
El análisis posterior para dicha variable podemos basarlo en ver
lo que pasa con la Figura 4.3 b) para lo cual se requiere
que el vértice de la parábola coincida con un punto de la
curva 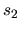 dentro del intervalo
dentro del intervalo 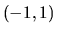 . Como el valor de
. Como el valor de
 para el vértice viene dado como
para el vértice viene dado como
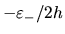 ,
entonces el valor de
,
entonces el valor de 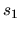 en ese punto será
en ese punto será
por lo tanto
Quedamos entonces en que la condición de tangencia es que se
igualen los valores de 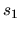 y
y 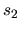 en el punto que estamos
considerando, por lo tanto calcularemos ahora el valor de
en el punto que estamos
considerando, por lo tanto calcularemos ahora el valor de 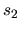
Para asegurarnos de que se trata del intervalo 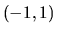 debemos
pedir que el denominador sea negativo, es decir
debemos
pedir que el denominador sea negativo, es decir
por consiguiente
eso es lo que deseamos, que el vértice de la
parábola esté entre las rectas 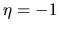 y
y 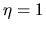 .
Además, no se olvide que necesitamos que
.
Además, no se olvide que necesitamos que 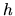 tome valores
negativos.
Hemos pedido mas arriba que se cumpla la igualdad
tome valores
negativos.
Hemos pedido mas arriba que se cumpla la igualdad 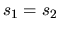 sin
embargo, tendremos otros casos para las relaciones
sin
embargo, tendremos otros casos para las relaciones 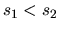 y
y
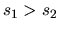 , tendremos por consiguiente, tres posibilidades, a
saber:
, tendremos por consiguiente, tres posibilidades, a
saber:
La primera relación corresponde a los casos que representamos por
la Figura 4.3 a) y vale para órbitas que comprenden a
los dos centros.
La segunda relación es para partículas que pueden girar
alternadamente en uno o en el otro centro describiendo trayectorias en
forma de ocho o algo por el estilo, eso depende del valor que tenga.
Finalmente, la tercera es para casos como los que representan en
las Figuras 4.3 c) y d), estos dos últimos casos son
fáciles de distinguir cuando el momento 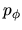 es nulo, lo
cual es equivalente a tener el movimiento en un plano. La
diferencia consistiría en que para un caso, las raíces
de la parábola estuvieran dentro del rango
es nulo, lo
cual es equivalente a tener el movimiento en un plano. La
diferencia consistiría en que para un caso, las raíces
de la parábola estuvieran dentro del rango 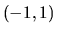 y para el
otro, una de esas raíces estaría fuera de dicho rango.
En caso de que
y para el
otro, una de esas raíces estaría fuera de dicho rango.
En caso de que 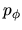 no sea cero, el procedimiento es
semejante, pero es menos directo porque depende también de la
energía que es la que determina el lado recto de la
parábola y no lo haremos aquí porque nuevamente surge el
problema de tratar con un polinomio de cuarto grado.
no sea cero, el procedimiento es
semejante, pero es menos directo porque depende también de la
energía que es la que determina el lado recto de la
parábola y no lo haremos aquí porque nuevamente surge el
problema de tratar con un polinomio de cuarto grado.




Next: Conclusiones.
Up: Algunos ejemplos de configuraciones
Previous: Energías negativas
Contents
Pedro Hernandez
2006-02-20