



Next: Algunos ejemplos
Up: Interpretación de algunos resultados
Previous: Interpretación de algunos resultados
Contents
-
- a)
- Gráficas de las coordenadas como funciones del tiempo.
En el capítulo 2 se discutió la subrutina GRAF que es
la encargada de realizar estas gráficas y sobre las
consideraciones de rangos de graficación, escalas, etc.
Veremos ahora con mayor cuidado un ejemplo: En el encabezado
están listados los valores de algunas de las constantes que
intervienen en el problema como son los valores iniciales, la
energía, la constante
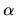 y los valores de las cargas,
según los valores de estas últimas, lo que podemos esperar es
que el movimiento tienda a desarrollarse del lado del segundo
centro, eso será favorecido también por el valor inicial del
momento asociado a la coordenada
y los valores de las cargas,
según los valores de estas últimas, lo que podemos esperar es
que el movimiento tienda a desarrollarse del lado del segundo
centro, eso será favorecido también por el valor inicial del
momento asociado a la coordenada  cuyo valor cero está
sobre el eje vertical que estamos representando por la letra
I. Las variaciones de la coordenada
cuyo valor cero está
sobre el eje vertical que estamos representando por la letra
I. Las variaciones de la coordenada 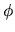 nos van a indicar
qué tan rápido es el giro de la partícula alrededor del
eje
nos van a indicar
qué tan rápido es el giro de la partícula alrededor del
eje 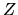 , en el ejemplo que estamos presentando lo que se nota es
que al final del intervalo que se considera aquí tiende a
girar cada vez mas rápido. Cuando el valor de una de las
coordenadas
, en el ejemplo que estamos presentando lo que se nota es
que al final del intervalo que se considera aquí tiende a
girar cada vez mas rápido. Cuando el valor de una de las
coordenadas  o
o  es constante entenderemos que el
movimiento ocurre sobre la superficie de un elipsoide o de un
hiperboloide aunque puede haber pequeñas desviaciones como en la
curva para la coordenada
es constante entenderemos que el
movimiento ocurre sobre la superficie de un elipsoide o de un
hiperboloide aunque puede haber pequeñas desviaciones como en la
curva para la coordenada  del ejemplo. Teniendo presente
todo lo que acaba de decirse, una vista rápida a la gráfica,
nos dice, que la partícula se acerca rápidamente en espiral
hacia el segundo centro que es lo que esperábamos; eso lo vamos
a ver en la siguiente gráfica.
del ejemplo. Teniendo presente
todo lo que acaba de decirse, una vista rápida a la gráfica,
nos dice, que la partícula se acerca rápidamente en espiral
hacia el segundo centro que es lo que esperábamos; eso lo vamos
a ver en la siguiente gráfica.
- b)
- Representación espacial del movimiento.
Las gráficas II y III nos permiten observar las órbitas para
los diferentes casos de interés en el problema. Mientras que las
curvas del inciso a) nos dan solamente una idea de lo que está
ocurriendo, aquí podemos tener una representación visual de
las trayectorias. La gráfica II es una proyección del
movimiento en el plano
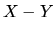 y la número III, la variación de
las coordenadas
y la número III, la variación de
las coordenadas 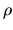 -
-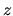 , donde
, donde 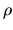 es el radio
cilíndrico y el eje
es el radio
cilíndrico y el eje 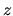 , es la línea donde están
colocados los dos centros, este último viene representado en la
gráfica por el eje horizontal, estando los dos centros en las
columnas 40 y 80 respectivamente; la variable
, es la línea donde están
colocados los dos centros, este último viene representado en la
gráfica por el eje horizontal, estando los dos centros en las
columnas 40 y 80 respectivamente; la variable 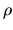 crece hacia
arriba y no toma valores negativos, como ya se sabe, esa es la
razón por la cual el cero para dicha variable se tomó al pie
de la página. Al observar estas gráficas, podemos comprobar lo
que se dijo en el inciso anterior; a medida que se desarrolla el
movimiento se observa que al final la partícula se precipita
hacia el segundo centro, eso se ve en la gráfica III, en la II
se oberva cómo la partícula gira alrededor del eje
crece hacia
arriba y no toma valores negativos, como ya se sabe, esa es la
razón por la cual el cero para dicha variable se tomó al pie
de la página. Al observar estas gráficas, podemos comprobar lo
que se dijo en el inciso anterior; a medida que se desarrolla el
movimiento se observa que al final la partícula se precipita
hacia el segundo centro, eso se ve en la gráfica III, en la II
se oberva cómo la partícula gira alrededor del eje 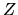 que
corresponde al origen de
que
corresponde al origen de 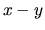 .
Un problema que se tiene con estas gráficas es que la escasa
resolución no permite construir fácilmente las órbitas
cuando aparecen muchos puntos, pero eso se corrige en parte si se
escoge un número pequeño de puntos para tener sólo una
porción pequeña de la trayectoria; desafortunadamente, el
número adecuado de puntos para cada caso, sólo puede
escogerse una vez que hemos obtenido una gráfica, así,
cuando deseamos tener una porción mejor definida de ella,
debemos correr por segunda vez el programa para ese ejemplo.
.
Un problema que se tiene con estas gráficas es que la escasa
resolución no permite construir fácilmente las órbitas
cuando aparecen muchos puntos, pero eso se corrige en parte si se
escoge un número pequeño de puntos para tener sólo una
porción pequeña de la trayectoria; desafortunadamente, el
número adecuado de puntos para cada caso, sólo puede
escogerse una vez que hemos obtenido una gráfica, así,
cuando deseamos tener una porción mejor definida de ella,
debemos correr por segunda vez el programa para ese ejemplo.
- c)
- Puntos de Retorno.
Hemos discutido también ya en otro capítulo este tipo de
gráficas. Recuérdese que los momentos
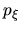 y
y 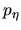 están expresados en función de raíces de polinomios de
cuarto grado. Estas gráficas corresponden precisamente a los
polinomios para
están expresados en función de raíces de polinomios de
cuarto grado. Estas gráficas corresponden precisamente a los
polinomios para  y para
y para  , a la primera se le representa
por el signo (+) y a la segunda por un asterisco. Como se ha
listado, tanto los valores de la variable como los de los dos
polinomios para cada punto de las gráficas es fácil determinar
con cierta presición para que valores de la variable las
gráficas cruzan al eje (puntos de retorno) así como los
valores que va tomando cada polinomio. Los únicos valores de la
coordenada que tiene sentido considerar desde un punto de vista
físico corresponden a aquellos para los cuales el
correspondiente polinomio no es negativo, de esa manera podemos
tener una idea de cuál es la región permitida, es decir, entre
que valores de
, a la primera se le representa
por el signo (+) y a la segunda por un asterisco. Como se ha
listado, tanto los valores de la variable como los de los dos
polinomios para cada punto de las gráficas es fácil determinar
con cierta presición para que valores de la variable las
gráficas cruzan al eje (puntos de retorno) así como los
valores que va tomando cada polinomio. Los únicos valores de la
coordenada que tiene sentido considerar desde un punto de vista
físico corresponden a aquellos para los cuales el
correspondiente polinomio no es negativo, de esa manera podemos
tener una idea de cuál es la región permitida, es decir, entre
que valores de  y de
y de  es posible tener confinada a una
partícula. Ya hemos dicho muchas veces y lo decimos una vez
más aquí, que sólo nos interesan los rangos en que puede
variar cada coordenada; con eso en mente, observamos que el rango
de valores permitido para la variable
es posible tener confinada a una
partícula. Ya hemos dicho muchas veces y lo decimos una vez
más aquí, que sólo nos interesan los rangos en que puede
variar cada coordenada; con eso en mente, observamos que el rango
de valores permitido para la variable  está comprendido
aproximadamente entre 1.4 y 1.7, en tanto que para
está comprendido
aproximadamente entre 1.4 y 1.7, en tanto que para  hay dos
rangos posibles: el primero está entre -0.9 y -0.4, mientras que
el segundo está entre 0.0 y 0.9. Con eso tenemos una idea de
cual es la región permitida: concluimos de nuestro análisis
que hay dos porciones del espacio en las cuales puede
desarrollarse el movimiento; todavía no tenemos una
representación visual, nos sucede lo mismo que con las curvas de
que hablamos en el inciso a) y de la misma manera que en aquel
caso, pasaremos a ver como se resuelve el problema, pero eso
corresponde al siguiente inciso.
hay dos
rangos posibles: el primero está entre -0.9 y -0.4, mientras que
el segundo está entre 0.0 y 0.9. Con eso tenemos una idea de
cual es la región permitida: concluimos de nuestro análisis
que hay dos porciones del espacio en las cuales puede
desarrollarse el movimiento; todavía no tenemos una
representación visual, nos sucede lo mismo que con las curvas de
que hablamos en el inciso a) y de la misma manera que en aquel
caso, pasaremos a ver como se resuelve el problema, pero eso
corresponde al siguiente inciso.
- d)
- Gráficas para la región permitida.
Como ya se dijo, esta gráfica es complementaria de la que
representa a los puntos de retorno, se vió en el apéndice (A)
cómo obtener dichas gráficas, así es que no insistiremos
más en eso. Lo que se tiene son una o varias zonas en blanco,
que representan a la región permitida, eso es en dos
dimensiones; para tres dimensiones basta con rotar la figura
alrededor del eje horizontal.
Hay que señalar que se está considerando el mismo caso para
explicar como hay que interpretar las gráficas, así es que
en el ejemplo V se verá todo lo que habíamos encontrado en
las gráficas del inciso c): existen dos zonas permitidas debido
a que hay dos rangos para
 , los valores de las coordenadas
pueden encontrarse de la manera siguiente: en la misma gráfica
se verá una serie de elipses y de hipérbolas las cuales
corresponden a diferentes valores de
, los valores de las coordenadas
pueden encontrarse de la manera siguiente: en la misma gráfica
se verá una serie de elipses y de hipérbolas las cuales
corresponden a diferentes valores de  y
y  ; los valores
de la primera están tomados en intervalos de 0.5 así que
entre dos elipses sucesivas el valor de
; los valores
de la primera están tomados en intervalos de 0.5 así que
entre dos elipses sucesivas el valor de  difiere por 0.5 en
tanto que para
difiere por 0.5 en
tanto que para  la diferencia entre dos hipérbolas es de
0.2. Ya con eso, no hay dificultad en determinar los rangos de
valores para
la diferencia entre dos hipérbolas es de
0.2. Ya con eso, no hay dificultad en determinar los rangos de
valores para  y para
y para  y verificar estos resultados con
los de las gráficas del inciso anterior, aunque aquí no es
muy precisa la escala; el estudio de estas gráficas es mas bien
cualitativo y sirve para visualizar los resultados de TURN.
Las gráficas tienen como encabezado los valores de algunas
constantes que intervienen en el problema. Se dan los valores que
tienen los momentos para ciertas
y verificar estos resultados con
los de las gráficas del inciso anterior, aunque aquí no es
muy precisa la escala; el estudio de estas gráficas es mas bien
cualitativo y sirve para visualizar los resultados de TURN.
Las gráficas tienen como encabezado los valores de algunas
constantes que intervienen en el problema. Se dan los valores que
tienen los momentos para ciertas  y
y  introducidas como
valores iniciales. Hay casos en que algún momento resulta imaginario,
apareciendo entonces un texto que así lo indica así como el
valor de el polinomio de cuarto grado que le corresponde, aunque en
ocasiones se da de todas maneras un valor para dicho momento pero eso
es porque en el programa se trabaja con el valor absoluto del polinomio.
En estas gráficas se puede ver como el cambio de una cualquiera de
esas constantes del problema afecta a la región permitida; en la
serie de gráficas presentadas aquí, lo que se ha variado es la
energía y puede verse claramente como se manifiesta eso en el
movimiento.
Conociendo la región permitida lo que puede hacerse es
seleccionar condiciones iniciales para el programa TWOC,
calculando los momentos para datos iniciales en las coordenadas,
previamente escogidos.
introducidas como
valores iniciales. Hay casos en que algún momento resulta imaginario,
apareciendo entonces un texto que así lo indica así como el
valor de el polinomio de cuarto grado que le corresponde, aunque en
ocasiones se da de todas maneras un valor para dicho momento pero eso
es porque en el programa se trabaja con el valor absoluto del polinomio.
En estas gráficas se puede ver como el cambio de una cualquiera de
esas constantes del problema afecta a la región permitida; en la
serie de gráficas presentadas aquí, lo que se ha variado es la
energía y puede verse claramente como se manifiesta eso en el
movimiento.
Conociendo la región permitida lo que puede hacerse es
seleccionar condiciones iniciales para el programa TWOC,
calculando los momentos para datos iniciales en las coordenadas,
previamente escogidos.
- e)
- Gráficas de las funciones:
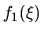 ,
, 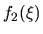 ,
, 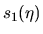 y
y 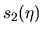 .
Acerca de estas funciones ya se discutió bastante, conocemos ya
todas sus variantes y en los ejemplos que vendrán después se
pondran apreciar algunas de ellas. En la práctica no
proporcionan ninguna información nueva, tal vez lo único
interesante sería el visualizar para casos concretos de qué
manera se comportan las curvas. Las funciones
.
Acerca de estas funciones ya se discutió bastante, conocemos ya
todas sus variantes y en los ejemplos que vendrán después se
pondran apreciar algunas de ellas. En la práctica no
proporcionan ninguna información nueva, tal vez lo único
interesante sería el visualizar para casos concretos de qué
manera se comportan las curvas. Las funciones 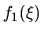 y
y
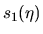 son representadas por el signo (+) en tanto que para
son representadas por el signo (+) en tanto que para
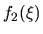 y
y 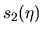 se escogió el signo (-) también se
grafica la recta de energía cero a la que se le representa
por puntos; se grafican los hechos que corresponden a las
posiciones -1 y +1 , los cuales son las asíntotas de
se escogió el signo (-) también se
grafica la recta de energía cero a la que se le representa
por puntos; se grafican los hechos que corresponden a las
posiciones -1 y +1 , los cuales son las asíntotas de
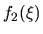 y
y 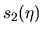 .
En los ejemplos que presentamos, se ha variado la energía de la
misma manera que para las gráficas del inciso d), de modo que para
cada gráfica de aquellas corresponde una parábola de estas dos
gráficas, recuérdese como influye la energía en las
características de las parábolas, así es que no es
difícil determinar la correspondencia de cada una de estas curvas
con cada una de las posibilidades de d). En los encabezados de las
gráficas se escribe entre otras cosas los valores de las coordenadas
para los que se han calculado los momentos en las gráficas para la
región permitida. Al igual que en todos los ejemplos anteriores, es
necesario tener presentes los rangos de validez para cada coordenada.
Después de estas observaciones ya no es difícil entenderlas.
Así como se varió la energía, se puede variar
también la constante
.
En los ejemplos que presentamos, se ha variado la energía de la
misma manera que para las gráficas del inciso d), de modo que para
cada gráfica de aquellas corresponde una parábola de estas dos
gráficas, recuérdese como influye la energía en las
características de las parábolas, así es que no es
difícil determinar la correspondencia de cada una de estas curvas
con cada una de las posibilidades de d). En los encabezados de las
gráficas se escribe entre otras cosas los valores de las coordenadas
para los que se han calculado los momentos en las gráficas para la
región permitida. Al igual que en todos los ejemplos anteriores, es
necesario tener presentes los rangos de validez para cada coordenada.
Después de estas observaciones ya no es difícil entenderlas.
Así como se varió la energía, se puede variar
también la constante 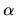 , o alguna de las que intervienen
como parámetros en nuestras funciones. En nuestro ejemplo no se
afectó la forma de
, o alguna de las que intervienen
como parámetros en nuestras funciones. En nuestro ejemplo no se
afectó la forma de 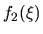 y
y 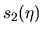 porque esas curvas
no dependen directamente de la energía pero un cambio en las
cargas magnéticas o en el momento
porque esas curvas
no dependen directamente de la energía pero un cambio en las
cargas magnéticas o en el momento 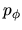 sí las va a
afectar; en el capítulo 1 se estudió qué papel desempeñan
esas constantes con respecto a las posiciones de las curvas.
sí las va a
afectar; en el capítulo 1 se estudió qué papel desempeñan
esas constantes con respecto a las posiciones de las curvas.
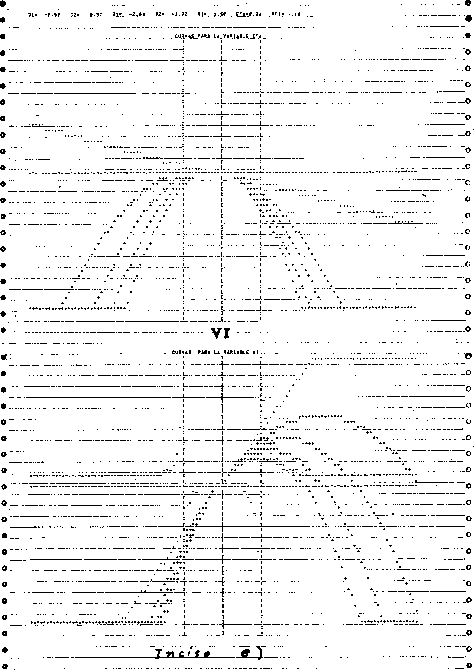
- f)
- Curvas de Energía Potencial Constante.
En el capítulo 3 se habló de la subrutina CNTU y en
el apéndice A, también se hizo mención a una subrutina
semejante para el programa PRYPO, esas son las gráficas
que presentaremos en nuestros ejemplos, es decir, las que se
obtienen con la subrutina REGP. Se considera el potencial
verdadero, o sea que no se incluye el potencial repulsivo mediante
el que era posible separar variables. Se tiene una colección de
franjas cuyos contornos corresponden a niveles de la misma
energía potencial. Se grafican los ejes verticales en las
posiciones -1 y 1 tanto para indicar la escala como para localizar
en donde están colocados los dos centros.
En esencia, ya no hay más qué decir sobre cómo entender las
gráficas. En seguida se tienen algunos ejemplos.
Figure C.1:
 |
Figure C.2:
 |
Figure C.3:
 |
Figure C.4:
 |
Figure C.5:
 |
Figure C.6:
 |




Next: Algunos ejemplos
Up: Interpretación de algunos resultados
Previous: Interpretación de algunos resultados
Contents
Pedro Hernandez
2006-02-20