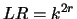Properties of reversible one dimensional cellular automata

Based on the work developed by Hedlund [Hed69], we can notice the following: um

Proposition 1   Reversible one dimensional cellular automata have the following properties:

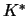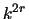1. Every finite sequence of states in the set ${K^{*}}$ have ${k^{2{r_{}}}}$ ancestors or finite sequences that generate it employing the evolution rule ${\varphi}$
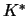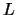2. The ancestors of every finite sequence in the set ${K^{*}}$ have $L$ different left sequences, 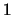$1$ unique central part and 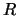$R$ different right sequences, holding that $LR={k^{2{r_{}}}}$

wi The first statement in Proposition 1 can be called the principle of uniform multiplicity of ancestors [McI91b]; and the values of $L$ and $R$ in the second statement are defined by Hedlund as the Welch indices [Hed69]. In this way, a reversible one dimensional cellular automaton holds that every sequence has the same number of ancestors that all the other sequences, and the ancestors of each sequence share a common central part , leaving the differences in the extremes.