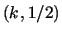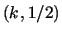Dynamical behavior of $({k^{}},1/2)$ reversible one dimensional cellular automata

In one dimensional cellular automata, we will consider the global mapping ${\Phi}$ among configurations of the configuration set ${{C}_{}}$ induced by an evolution rule ${\varphi}$ as the mapping generating the dynamical behavior in the configuration space ${({{C}_{}},{\mathfrak{C}_{}})}$.

The orbit described by any configuration is the progressive evolution produced by the iteration of the global mapping ${\Phi}$ over the same configuration, and the regions that this orbit visits are the cylinder sets covering the configuration set ${{C}_{}}$.

Right now a complete characterization of one dimensional cellular automata doesn't exists. For this reason is very difficult to know which are the conditions for classifying the evolution of a one dimensional cellular automaton, doesn't matter the simplicity of its evolution rule. However, for the reversible case we have this characterization as we see in section 3. This result will be used to define some matrix methods for detecting the kind of orbits described in section 4.

We only analyse the case of $({k^{}},1/2)$ reversible one dimensional cellular automata because all the cases can be simulated whit this kind of automata.