



Next: Detecting transitive behavior in
Up: Dynamical behavior of reversible
Previous: Detecting some periodical behavior
Contents
Transitive behavior of
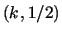 reversible one dimensional cellular automata
reversible one dimensional cellular automata
We have seen that some restrictions in the configurations define both periodic orbits and non-wandering centered cylinder sets in
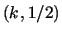 reversible one dimensional cellular automata. Now is desirable to consider not only one but all the possible mappings that a sequence
reversible one dimensional cellular automata. Now is desirable to consider not only one but all the possible mappings that a sequence
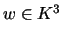 has to. This can be done using again block permutations and the process is the following:
has to. This can be done using again block permutations and the process is the following:
- For a sequence
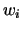 of states in the set
of states in the set 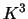 , take its mapping to an unique block
, take its mapping to an unique block 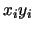 using the block permutation
using the block permutation  .
.
- Associate the element
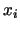 with all the elements
with all the elements 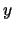 in the set
in the set  and the element
and the element 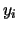 with all the elements
with all the elements  in the set
in the set  .
.
- With the associations
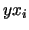 and
and  and using the block permutation
and using the block permutation 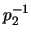 , form the respective list of the mappings from these associations to sequences
, form the respective list of the mappings from these associations to sequences 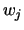 and
and 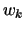 of states in the set
of states in the set 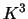 .
.
- Using the block permutation
 , every list of sequences
, every list of sequences 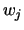 and
and 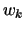 of states defined by
of states defined by 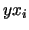 and
and  , maps respectively to a list of blocks with the form
, maps respectively to a list of blocks with the form 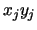 and
and  .
.
- From the last lists, take only all the different elements
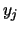 in the first list and all the different elements
in the first list and all the different elements 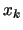 in the second list.
in the second list.
- Form the cartesian product of such lists. This cartesian product form a new list of blocks with the form
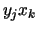 .
.
- The list of blocks
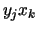 maps to a list of sequences
maps to a list of sequences 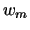 using the block permutation
using the block permutation 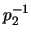 . Thus, we have a subset of the set
. Thus, we have a subset of the set 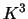 .
.
In this way, we have that an initial sequence 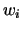 maps to a set of sequences
maps to a set of sequences 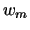 placed in the same position and therefore we have all the possible mappings from sequences to sequences in the set
placed in the same position and therefore we have all the possible mappings from sequences to sequences in the set 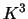 as is showed in Figure 12.
tr
as is showed in Figure 12.
tr
Figure 12:
Description of all the possible mappings from a sequence 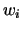 to a set of sequences
to a set of sequences 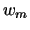 using block permutations
using block permutations
|
|
Using all the sequences  of states in the set
of states in the set 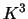 for defining centered cylinder sets
for defining centered cylinder sets
![$ {\mathcal{C}_{[{w_{}}]}}$](img120.gif) , the previous process defines the possible mappings from a centered cylinder set to other centered cylinder sets. In this way, we can use this process for detecting transitive behavior among centered cylinder sets that cover all the configuration space
, the previous process defines the possible mappings from a centered cylinder set to other centered cylinder sets. In this way, we can use this process for detecting transitive behavior among centered cylinder sets that cover all the configuration space
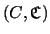 .
.




Next: Detecting transitive behavior in
Up: Dynamical behavior of reversible
Previous: Detecting some periodical behavior
Contents
ice
2001-09-01
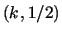 reversible one dimensional cellular automata
reversible one dimensional cellular automata
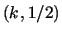 reversible one dimensional cellular automata
reversible one dimensional cellular automata
![]() reversible one dimensional cellular automata. Now is desirable to consider not only one but all the possible mappings that a sequence
reversible one dimensional cellular automata. Now is desirable to consider not only one but all the possible mappings that a sequence
![]() has to. This can be done using again block permutations and the process is the following:
has to. This can be done using again block permutations and the process is the following:
![]() maps to a set of sequences
maps to a set of sequences ![]() placed in the same position and therefore we have all the possible mappings from sequences to sequences in the set
placed in the same position and therefore we have all the possible mappings from sequences to sequences in the set ![]() as is showed in Figure 12.
tr
as is showed in Figure 12.
tr
![\includegraphics[width=4in]{imagenes/transitivity}](img147.gif)
![]() of states in the set
of states in the set ![]() for defining centered cylinder sets
for defining centered cylinder sets
![]() , the previous process defines the possible mappings from a centered cylinder set to other centered cylinder sets. In this way, we can use this process for detecting transitive behavior among centered cylinder sets that cover all the configuration space
, the previous process defines the possible mappings from a centered cylinder set to other centered cylinder sets. In this way, we can use this process for detecting transitive behavior among centered cylinder sets that cover all the configuration space
![]() .
.