



Next: A chain of references
Up: Putzer's Method
Previous: Reduction of a power
It still remains to describe the transition from the reduction of the power series for f modulo the characteristic polynomial to Sylvester's formula. To do that it is convenient to factor the characteristic polynomial
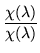 |
= |
1 |
(16) |
in which the quotient
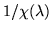 is first resolved into partial fractions, and then multiplied by the numerator
is first resolved into partial fractions, and then multiplied by the numerator
 to get a sum of terms Gi which are characterized as arising from that part of the partial fraction depending upon the denominator
to get a sum of terms Gi which are characterized as arising from that part of the partial fraction depending upon the denominator
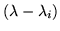 .
If
.
If 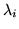 is simple,
is simple,
| Gi |
= |
 |
(17) |
otherwise it might be multiplied by a polynomial in
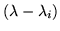 whose degree would be less than the multiplicity ri. The point is that the
whose degree would be less than the multiplicity ri. The point is that the
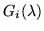 resolve the identity, and so do their matrix counterparts:
resolve the identity, and so do their matrix counterparts:
 |
= |
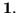 |
(18) |
Nevertheless each of them can be multiplied by a power of
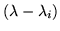 sufficient to create the characteristic polynomial, which vanishes for the matrix M, meaning that for some p,
sufficient to create the characteristic polynomial, which vanishes for the matrix M, meaning that for some p,
If this resolution of the identity is applied to the power series representation of a function, there results
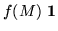 |
= |
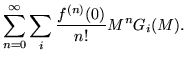 |
(21) |
After changing the order of summation, it would be preferable to have the expansion of f about each eigenvalue, to be consistent with the operation of each Gi on the terms of the series. The shift is accomplished by writing
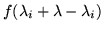 |
= |
 |
(22) |
whose immediate matricial counterpart is
| f(M) |
= |
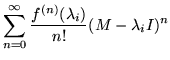 |
(23) |
| |
= |
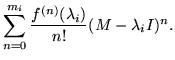 |
(24) |
The series at each eigenvalue has been truncated, according to the power of
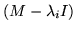 needed as a multiplier of Gi(M) to complete the characteristic polynomial. But this is nothing more than a derivation of equation 5, in which the derivatives of f replace the combinations of coefficients of f and elements of powers of the companion matrix.
needed as a multiplier of Gi(M) to complete the characteristic polynomial. But this is nothing more than a derivation of equation 5, in which the derivatives of f replace the combinations of coefficients of f and elements of powers of the companion matrix.
The fact that the Gi omit terms in 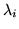 but have the full complement of remaining factors from
but have the full complement of remaining factors from 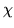 ensures that GiGj=0 for
ensures that GiGj=0 for 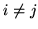 ;
this together with the fact that the Gi resolve the identity ensures Gi2=G1.
We therefore have a set of commuting orthogonal idempotents, which are projectors onto the eigenvalue subspaces. We can even claim that
;
this together with the fact that the Gi resolve the identity ensures Gi2=G1.
We therefore have a set of commuting orthogonal idempotents, which are projectors onto the eigenvalue subspaces. We can even claim that
| Ni(k) |
= |
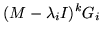 |
(25) |
are the nilpotents of equation 5, and that they satisfy
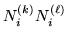 |
= |
 |
(26) |
The rows and columns of the matrices Ni(k) are eigenvectors and members of the Jordan chains by which the canonical form of M may be exhibited. They still have to be sorted out when there are several linearly independent eigenvectors belonging to the same eigenvalue, something which can be done with the help of the minimal polynomial. An unexpected aspect of Putzer's method lies in its avoidance of all those details on account of the fact that the general Sylvester's formula only requires the idempotents and nilpotents, without needing to identify the vectors in a Jordan basis explicitly.




Next: A chain of references
Up: Putzer's Method
Previous: Reduction of a power
root
2000-03-17

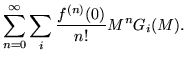

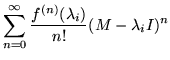
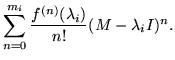
![]() but have the full complement of remaining factors from
but have the full complement of remaining factors from ![]() ensures that GiGj=0 for
ensures that GiGj=0 for ![]() ;
this together with the fact that the Gi resolve the identity ensures Gi2=G1.
We therefore have a set of commuting orthogonal idempotents, which are projectors onto the eigenvalue subspaces. We can even claim that
;
this together with the fact that the Gi resolve the identity ensures Gi2=G1.
We therefore have a set of commuting orthogonal idempotents, which are projectors onto the eigenvalue subspaces. We can even claim that