| f(M) | = | 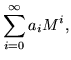 |
(10) |
Of course, the matrix version of an analytic function could just be defined by its power series,
| f(M) | = | 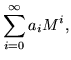 |
(10) |
Since a matrix satisfies its own characteristic equation,
| Mn | = | 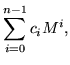 |
(11) |
The reduction can actually be performed by using the companion matrix of M,
![$\displaystyle \left[ \begin{array}{cccccc}
{\bf0}& {\bf 1}& {\bf0}& \ldots & {\...
...}{c}
I \\
M \\
M^2 \\
\ldots \\
M^{n-2} \\
M^{n-1} \\
\end{array} \right]$](img49.gif) |
= | ![$\displaystyle \left[ \begin{array}{c}
M \\
M^2 \\
M^3 \\
\ldots \\
M^{n-1} \\
M^{n} \\
\end{array} \right]$](img50.gif) |
(12) |
Call C the matrix in this equation, which is a Kronecker product of the companion matrix with the ![]() identity matrix, and V the vector formed by the first few powers of M, which is also a Kronecker product. Since M is an eigenvalue of C with eigenvector V, it follows
identity matrix, and V the vector formed by the first few powers of M, which is also a Kronecker product. Since M is an eigenvalue of C with eigenvector V, it follows
| f(M)V | = | f(C)V. | (13) |
Consequently, it is only necessary to read off the first row of f(C)V to get f(M) as a linear combination of the low powers of M. However, this result still requires summing a whole power series, so it may offer no advantages as a numerical procedure. The essence of Putzer's method, which is dedicated to calculating matrix exponentials, lies in obtaining eCt as the solution of a differential equation, then deducing eMt. While a meritorious route to solving to this particular application, the unwary might not notice that the Jordan decompositions for M and C need not coincide, and yet the method still yields a true result.
The companion matrix C is not a canonical form, because its Jordan blocks have dimension equal to the multiplicity of each eigenvalue, whereas those of M may decompose into smaller blocks in any way which is consistent with the overall multiplicity. They keep the same symmetric functions and hence the same companion matrix, even though equivalence through a change of basis would want to write the companion matrix as a direct sum of smaller companion matrices. On the other hand, C maximizes any other arrangement by containing all the other Jordan subspaces, which is why the numerical methods work; nilpotents in the full Sylvester's formula will all have expired by the time their presence could have caused any interference.
In subsequent articles some commentaries on the method were published, but the general context of canonical forms seems to have been overlooked in the pursuit of minor improvements and extensions. Since the coefficients of the companion matrix are symmetric functions of the eigenvalues of M, it might seem that the eigenvalues could be put to better use by just evaluating f rather than starting up a whole new procedure. However, all that can be avoided by observing that the symmetric functions can be obtained directly by using the traces of low powers.
Since those matrices are going to be used anyway, taking their traces represents little additional labor. There is a series of identities relating power sums to symmetric functions due to Newton,
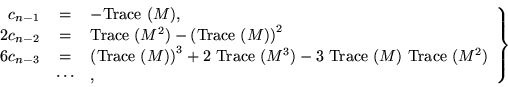 |
(14) |
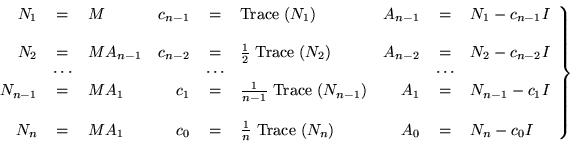 |
(15) |