 |
Having decided to represent cellular automata with the aid of paths in a diagram, not only is it found that there are several kinds of diagrams to work with, but that the properties of the diagrams are reflected in their topological connection matrices. In that respect, the study of cellular automata turns into an exercise in linear algebra, at least to the extent that such machinery as eigenvalues, eigenvectors, canonical forms and the representation of mappings by matrices is concerned.
In order to fix our attention on a concrete example, consider the reversible (3,1/2) cellular automaton numbered, in Wolfram's scheme, 14937.
 |
Figure 4 shows a typical portion of an evolutionary sequence. The rule has been chosen to make every state quiescent, an option that is always available for reversible automata, making the remainder of the evolution stand out more clearly. Total quiescence means that the states run in order along the diagonal of the evolution matrix, which is shown over to the right in the same figure.
Uniform multiplicity is evident in the matrix when the number of times that a state is listed there is the same for all states; in this case three times each. That works out to once per row and once per column, but this example shows it is only by the average, and not always in detail.
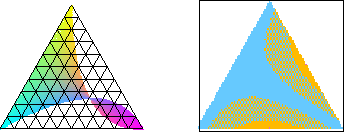 |
Examination of the mean field probabilities is a standard procedure in the assay of any new automaton. For reversible automata, one suspects that concentrations of one state or another will never be seen because that would go against the uniform multiplicity of ancestors. However, generation to generation exchanges of probabilities certainly occur because permutations, practically be definition, will not upset the balance of ancestors.
In the left portion of Figure 5 in which states 0 and 1 lie along the base in that order from left to right, state 2 sits at the apex. The rule tends to exchange 0 and 2, leaving 1 fixed. In the right half of the figure, a contour plot is shown in which fixed points of probability would manifest as zeroes. Without having some other rules available for comparison, it is only slightly evident that there is an extended saddle point encompassing the whole of the triangle of actual probabilities.