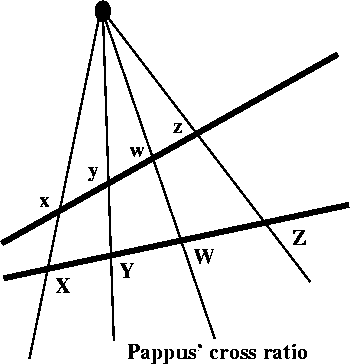
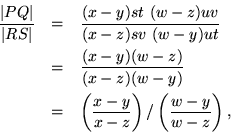Books on projective geometry depend heavily on the invariance of cross ratio with respect to linear fractional transformations, as do books on complex analysis. Verifying the invariance is customarily assigned as an exercise, but there seems to be almost no discussion of the sources of the cross ratio. As a result from the geometry of antiquity, its proof involves the comparison of similar triangles, but not much is said about the possible origins of those triangles in perspective drawings.
In our recent work the issue has come up in two places. First, the programs PHOC and SHOC, which are based on the books of E. A. Maxwell [4,5], consist of a series of demonstrations based on exercises or theorems in the books. Since these rely heavily on the cross ratio, there is a natural element of curiosity regarding its origins. The most recent encounter with the elements of projective geometry has been in a course in mathematical methods. In the linear algrbra portion, there is a natural progression from linear spaces to affine spaces to projective spaces, especially during the development of group representation theory, where the cross ratio comes up in the study of projective invariants. In the complex analysis portion of the course, explaining the role of fractional linear transformations leads to the same interest in cross ratios.
Consider the projective line as an image of a two-dimensional linear algebra plane, and observe that determinants are multiplicative for linear transformations. Take a ![]() matrix P containing the two columns of a basis and a transformation M. Then
|MP|=|M||P|, so |P| is not an invariant. But take another basis matrix Q for which
|MQ|=|M||Q|. Then the quotient |P|/|Q| is invariant, although its terms are not.
matrix P containing the two columns of a basis and a transformation M. Then
|MP|=|M||P|, so |P| is not an invariant. But take another basis matrix Q for which
|MQ|=|M||Q|. Then the quotient |P|/|Q| is invariant, although its terms are not.
 |
Carrying the result over to the projective line, write the matrices in projective form
Although this quotient is invariant enough, the multipliers would normally be unknown. Choosing more vectors and dividing once again would only create more multipliers, but the same multipliers can be kept by just rearranging the four vectors in the two bases. There are twenty four possibilities, the permutations of four objects, but only four of them produce the cancellation which would free the points from the multipliers.
The nice symmetry of the formula shows how to get the cancellation; note that each difference is multiplied by the product of its two multipliers. Making up a product of four multipliers in two different ways would allow cancelling the unknown factors while retaining the differences in the points themselves.
So, make up two new matrices,