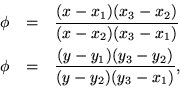Relative distance interpretation

The derivation of the cross ratio given in the last subsection was based on determinants in the plane, according to which it is really a result about areas, likewise in the plane. The drawing for Pappus's construction also uses a plane, although only as a device to illustrate a one-to-one reversible mapping between two lines gotten by drawing lines out from a focus, to see where they intersect a couple of lines.

Confined to the interior of a line, the invariance of the cross ratio tells something about trying to locate a point by specifying its relative distance from a pair of reference points. Under an affine transformation, which would be a combination of dilation and translation, that ought to suffice. By projective transformation, where the dilation is not uniform, it is the ratio of ratios which is invariant. In other words, if it is $\rho$ times as far from w to x as it is from w to y, and it is $\sigma$ times as far from z to x as it is from z to y (all of this being taken with due regard for sign), then the ratio of $\sigma$ to $\rho$ will always be the same, even when $\rho$ and $\sigma$ are not.

To give this a still more concrete interpretation, suppose that w is the midpoint between x and y. It probably isn't still the midpoint after projection, although if two points were halfway between, they would have to move together. Trisectors of an interval, w and z with ratios of 2:1 and 1:2 probably won't map into trisectors either, but the quotient 4 would have to be respected. And so on.

To summarize a long series of special cases, observe that although a cross ratio is unaffected by whatever projective transformation, its particular value still depends on the four points chosen. It is a reasonable question, given the cross ratio and three of the points, to ask for the fourth. Put

$$\begin{eqnarray*}\sigma & = & \frac{w-z}{w-y} \end{eqnarray*}$$

to get, for cross ratio $\phi$,

$$\begin{eqnarray*}\phi & = & \frac{(x-y)(w-z)}{(x-z)(w-y)} \\ x & = & \frac{\phi z - y \sigma}{\phi - \sigma} \end{eqnarray*}$$

The invariance of the cross ratio can be used much less explicitly. Suppose that it is desired to map points x₁, x₂, x₃ into points y₁, y₂, y₃, and to find the consequences for other points. Note that for whatever value of $\phi$ arising from x, x₁, x₂, x₃, there is always a y determined by the same $\phi$ and further values y₁, y₂, y₃. Using that common value of the cross ratio and unknown points x and y, we get

$$\begin{eqnarray*}\phi & = & \frac{(x-x_1)(x_3-x_2)}{(x-x_2)(x_3-x_1)} \\ \phi & = & \frac{(y-y_1)(y_3-y_2)}{(y-y_2)(y_3-x_1)}, \end{eqnarray*}$$

so the equation for the mapping would be

 

$$\frac{(x-x_1)(x_3-x_2)}{(x-x_2)(x_3-x_1)} \frac{(y-y_1)(y_3-y_2)}{(y-y_2)(y_3-y_1)}.$$ = (1)

It can be checked by substitution and, if necessary, the use of l'Hospital's rule.