 |
 |
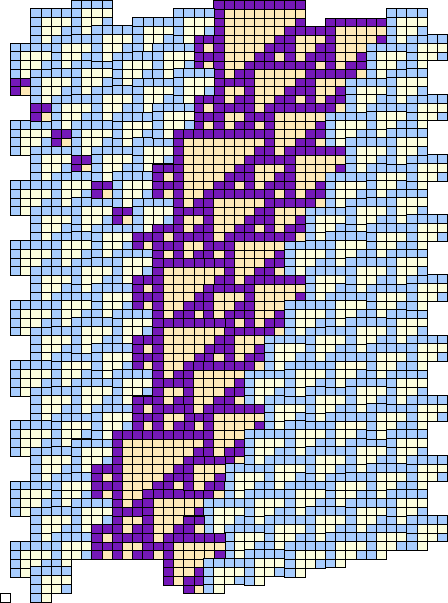
Cook recognizes at least seven types of gliders, some of which have multiple variants, and all of which can be packed in various combinations. Glider technology consists in exploiting collisions. It is readily seen that there are fifty or more, actually in the hundreds or thousands, of binary collisions. From there on the numbers are much larger. Although that forebodes a mass of data, there is an element of hope.
 |
Even though a dozen or two of gliders seems like a large number, that is far fewer than the number of possible collisions. Either collisions will produce multiple reaction products, or many collisions will end up producing identical results. Both alternatives coexist, but one of the fortunate combinations leaves the reactants unchanged, just that they chang places. That is a soliton reaction, useful for moving information from one place to another across intervening barriers.
Actually we didn't discover this for ourselves, but only as a result of a hint from Cook. That, and the general knowledge that it would eventually be necessary to examine the collisions in one way or another.
 |
 |
 |
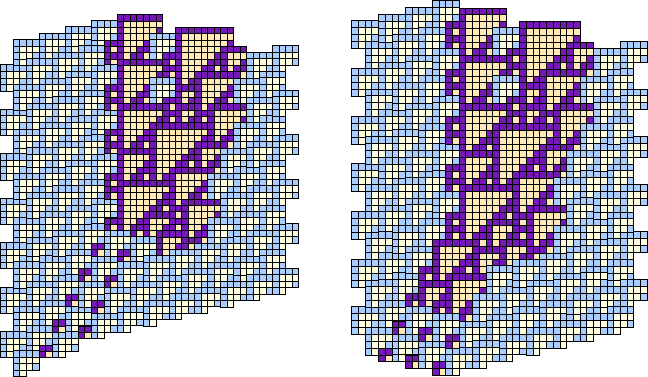
Part of the understanding of E and G collisions is that the leading triangles are escorting ![]() gliders in one constellation or another; when the escort is damaged by a collision, the result is a typical putrefaction of an
gliders in one constellation or another; when the escort is damaged by a collision, the result is a typical putrefaction of an ![]() lattice, for which the rules of engagement can be worked out.
lattice, for which the rules of engagement can be worked out.