



Next: Reduction of a power
Up: Putzer's Method
Previous: Background
The starting point for proving theorems about matrices is to establish the Cayley-Hamilton theorem, and to understand some of its corrolaries, such as theexistence and meaning of eigenvalues and eigenvectors. A good way to do this is to work with the resolvent,
whose properties depend on the vanishing or nonvanishing of the determinant
which is well known to be a polynomial in 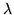 with no more roots than the dimension of M, and exactly that number when multiplicity is taken into account. The reason that roots are involved is that eigenvectors, for which
with no more roots than the dimension of M, and exactly that number when multiplicity is taken into account. The reason that roots are involved is that eigenvectors, for which
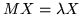 ,
have to avoid appearing to satisfy
,
have to avoid appearing to satisfy
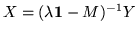 for Y=0. They do so by being annihilated by the inverse of the resolvent, featuring the eigenvalues as locations where the resolvent itself cannot be formed.
for Y=0. They do so by being annihilated by the inverse of the resolvent, featuring the eigenvalues as locations where the resolvent itself cannot be formed.
The resolvent of any finite matrix has an explicit form which transforms an expression involving powers of 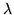 into one involving powers of the matrix. Looking at the adjugate (which is almost the inverse) of
into one involving powers of the matrix. Looking at the adjugate (which is almost the inverse) of
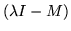 ,
observe that it is a polynomial of degree n-1 in
,
observe that it is a polynomial of degree n-1 in 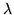 because that is the maximum dimension of the cofactors and thus the maximum number of
because that is the maximum dimension of the cofactors and thus the maximum number of 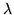 s which could ever be multiplied together. Putting coefficients of
s which could ever be multiplied together. Putting coefficients of 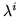 together in a matrix called Ai, set
together in a matrix called Ai, set
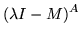 |
= |
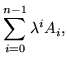 |
(6) |
with a corresponding expansion of the characteristic polynomial
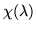 |
= |
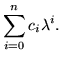 |
(7) |
Then the equation
could be subjected to a series of transformations
to get a result in which the matrix coefficient of each power of 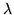 would have to vanish. That produces a chain of substitutions:
would have to vanish. That produces a chain of substitutions:
The missing A-1, as well as the nonexistent An would both have to be O. Written out in greater detail,
All these equations are readily summarized in one single matrix equation,
![$\displaystyle \left[ \begin{array}{c}
O \\ A_0 \\ \ldots \\ A_{n-3} \\ A_{n-2} \\ A_{n-1} \end{array} \right]$](img44.gif) |
= |
![$\displaystyle \left[ \begin{array}{cccccc}
c_0 & c_1 & c_2 & & c_{n-1} & c_n \\...
...ray}{c}
I \\ M \\ \ldots \\ M^{n-2} \\ M^{n-1} \\ M^n \end{array} \right].$](img45.gif) |
(9) |
In fact, cn=1, so that the last equation of the series asserts that
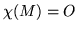 ,
which is just the Cayley-Hamilton Theorem: a matrix satisfies its own characteristic equation.
,
which is just the Cayley-Hamilton Theorem: a matrix satisfies its own characteristic equation.




Next: Reduction of a power
Up: Putzer's Method
Previous: Background
root
2000-03-17
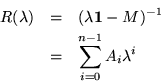
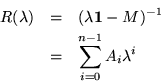
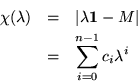
![]() into one involving powers of the matrix. Looking at the adjugate (which is almost the inverse) of
into one involving powers of the matrix. Looking at the adjugate (which is almost the inverse) of
![]() ,
observe that it is a polynomial of degree n-1 in
,
observe that it is a polynomial of degree n-1 in ![]() because that is the maximum dimension of the cofactors and thus the maximum number of
because that is the maximum dimension of the cofactors and thus the maximum number of ![]() s which could ever be multiplied together. Putting coefficients of
s which could ever be multiplied together. Putting coefficients of ![]() together in a matrix called Ai, set
together in a matrix called Ai, set
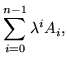
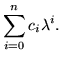
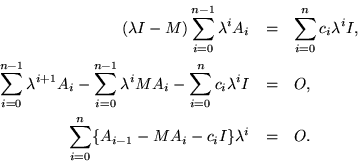
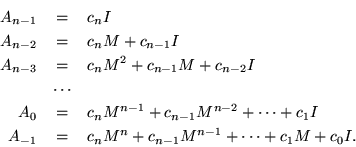
![$\displaystyle \left[ \begin{array}{c}
O \\ A_0 \\ \ldots \\ A_{n-3} \\ A_{n-2} \\ A_{n-1} \end{array} \right]$](img44.gif)
![$\displaystyle \left[ \begin{array}{cccccc}
c_0 & c_1 & c_2 & & c_{n-1} & c_n \\...
...ray}{c}
I \\ M \\ \ldots \\ M^{n-2} \\ M^{n-1} \\ M^n \end{array} \right].$](img45.gif)
![]() ,
which is just the Cayley-Hamilton Theorem: a matrix satisfies its own characteristic equation.
,
which is just the Cayley-Hamilton Theorem: a matrix satisfies its own characteristic equation.