




Next: Definición de Espacios Sóficos
Up: Introducción al Espacio de
Previous: Corrimientos de Tipo Finito
Contenido
Indice
Un paso acostumbrado en dinámica simbólica es repre-sentar un corrimiento de tipo finito por medio de una gráfica , donde todas las posibles rutas del diagrama muestren la colección de las secuencias que se tienen en
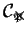 , para autómatas celulares lineales, la gráfica que resulta natural para conocer las evoluciones del conjunto
, para autómatas celulares lineales, la gráfica que resulta natural para conocer las evoluciones del conjunto
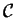 es el diagrama de de Bruijn [McI91].
es el diagrama de de Bruijn [McI91].
Para un autómata celular con 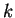 estados y un radio de vecindad
estados y un radio de vecindad 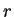 , la definición del diagrama de de Bruijn es la siguiente:
, la definición del diagrama de de Bruijn es la siguiente:
- El conjunto de nodos del diagrama de de Bruijn
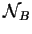 consistirá de todas las posibles secuencias de estados de longitud
consistirá de todas las posibles secuencias de estados de longitud 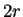 , es decir,
, es decir,
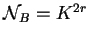 .
.
- Para
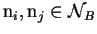 , existirá una arista de
, existirá una arista de
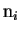 a
a
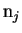 si los
si los 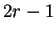 elementos finales de
elementos finales de
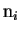 son iguales a los
son iguales a los 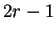 elementos iniciales de
elementos iniciales de
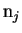 , para el caso en que
, para el caso en que 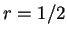 , tenemos 0 elementos finales para
, tenemos 0 elementos finales para
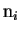 y 0 elementos iniciales para
y 0 elementos iniciales para
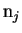 , por lo que en esta situación en particular el diagrama será completo.
, por lo que en esta situación en particular el diagrama será completo.
- Cada arista en el diagrama de de Bruijn representa una vecindad del autómata, es decir, un bloque de estados de longitud
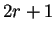 , tomando en cuenta el elemento inicial del nodo
, tomando en cuenta el elemento inicial del nodo
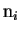 , el traslape de longitud
, el traslape de longitud 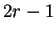 y el elemento final del nodo
y el elemento final del nodo
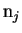 . Al conjunto de aristas del diagrama de de Bruijn se le denominará con
. Al conjunto de aristas del diagrama de de Bruijn se le denominará con
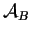 y representa al conjunto de vecindades
y representa al conjunto de vecindades 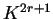 de un autómata celular lineal.
de un autómata celular lineal.
- Cada arista
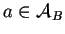 se etiquetará con un símbolo o se coloreará con un color distinguiendo el estado en el cual evoluciona la vecindad representada por
se etiquetará con un símbolo o se coloreará con un color distinguiendo el estado en el cual evoluciona la vecindad representada por 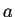 , o sea, el etiquetado de todas las aristas representa al mapeo
, o sea, el etiquetado de todas las aristas representa al mapeo
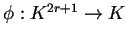 que es la regla de evolución del autómata.
que es la regla de evolución del autómata.
Figura 12:
Diagramas de de Bruijn genéricos.
|
|
Por medio del diagrama de de Bruijn, tenemos una re-presentación gráfica de la regla de evolución, las rutas en este diagrama representan todas las posibles configuraciones que aparecen en la evolución del autómata celular como producto de 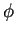 .
.
Cabe señalar que en la literatura sobre dinámica simbólica, el uso del diagrama de de Bruijn es casi inexis-tente, prefiriendo usar otro tipo de diagramas más a la manera de la representación gráfica de autómatas finitos, o la gráfica dual del diagrama de de Bruijn (en caso de existir).





Next: Definición de Espacios Sóficos
Up: Introducción al Espacio de
Previous: Corrimientos de Tipo Finito
Contenido
Indice
ice
2001-08-30
![]() , para autómatas celulares lineales, la gráfica que resulta natural para conocer las evoluciones del conjunto
, para autómatas celulares lineales, la gráfica que resulta natural para conocer las evoluciones del conjunto
![]() es el diagrama de de Bruijn [McI91].
es el diagrama de de Bruijn [McI91].
![]() estados y un radio de vecindad
estados y un radio de vecindad ![]() , la definición del diagrama de de Bruijn es la siguiente:
, la definición del diagrama de de Bruijn es la siguiente:
![]() .
.