


Next: Bibliograf´ia
Up: INSTITUTO POLITÉCNICO NACIONAL ESCUELA
Previous: Grupo de simetría cuántico
Contents
La sección de conclusiones es, en cierto sentido, la más personal
de un trabajo. Por ésto, cambiaré el tono más o menos impersonal del
lenguaje usado en las secciones anteriores, más técnicas. Enumeraré a
continuación las conclusiones que considero más relevantes sobre la
presente tesis.
1.
En la Introducción, las ecuaciones (3,4) son generalizaciones
de las (1,2) las cuales no tienen más base que un propósito de
simetrización; por lo tanto, los resultados que se obtienen de su
aplicación tienen tan sólo este fundamento. Entonces, la
definición misma de monopolo magnético no es obvia. Por ejemplo,
se puede definir un monopolo magnético puntual como ``algo" cuya
presencia implica la veracidad de la cuarta de las ecuaciones (3) de
la Introducción en el punto en el cual se supone su existencia; en
este caso, integrando la ecuación mencionada en una esfera de
radio 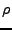 , aplicando consideraciones de simetría radial y la
expresión para la fuerza de Lorentz generalizada ( o sea,
siguiendo un procedimiento análogo al empleado en Electrostática
para obtener la ley de Coulomb a partir de la de Gauss), se obtiene
una expresión para la fuerza entre dos monopolos magnéticos
análoga a la obtenida en el caso eléctrico, la cual indica que
dos monopolos con igual signo se repelen y dos con signos contrarios
se atraen. Sin embargo, algunas personas, como Miller y
Gamblin [73], partiendo de consideraciones un poco distintas a
las referentes puramente a razones de simetría, han obtenido
resultados más bien inesperados: Gamblin [73] requiriendo la
existencia de un principio de acción (densidad Lagrangiana)
satisfactorio, obtiene, de las ecuaciones del campo, el resultado
de que monopolos de signos iguales se deben atraer, existiendo
repulsión entre los signos opuestos; este resultado esta en
oposición completa al mencionado anteriormente.
, aplicando consideraciones de simetría radial y la
expresión para la fuerza de Lorentz generalizada ( o sea,
siguiendo un procedimiento análogo al empleado en Electrostática
para obtener la ley de Coulomb a partir de la de Gauss), se obtiene
una expresión para la fuerza entre dos monopolos magnéticos
análoga a la obtenida en el caso eléctrico, la cual indica que
dos monopolos con igual signo se repelen y dos con signos contrarios
se atraen. Sin embargo, algunas personas, como Miller y
Gamblin [73], partiendo de consideraciones un poco distintas a
las referentes puramente a razones de simetría, han obtenido
resultados más bien inesperados: Gamblin [73] requiriendo la
existencia de un principio de acción (densidad Lagrangiana)
satisfactorio, obtiene, de las ecuaciones del campo, el resultado
de que monopolos de signos iguales se deben atraer, existiendo
repulsión entre los signos opuestos; este resultado esta en
oposición completa al mencionado anteriormente.
Lo anterior, da una idea de tipo de dificultades que se tienen en la
construcción de una teoría de partículas
hipotéticas: distintos requerimientos implican teorías con
resultados en ocasiones opuestos. Sin embargo, se necesita, en
cada caso, una base de partida; en el caso de monopolos
magnéticos, me parece que la original, consiste en razones de
simetría, es la más satisfactoria.
Se debe tener en cuenta, entonces, la base, débil, sobre la cual se
hace la generalización de las ecuaciones (1,2) a las (3,4) de la
introducción. esto implica especiales dificultades para la
detección experimental de monopolos magnéticos; en cualquier
arreglo diseñado para este fín, se trata de identificarlos
por alguna propiedad particular ( por ejemplo, la fuerza de
Lorentz sobre ellos en el campo electrico de un condensador o la
corriente eléctrica a que dan lugar según la Ley de Farady);
sin embargo, puede ser que una de las fallas fundamentales en los
métodos experimentales empleados hasta hoy el hecho de suponer
de los monopolos propiedades que realmente no tienen. En este
caso, debido a que se debe suponer algo respecto a ellos para
poder principiar su estudio, no queda más remedio que probar la
mayor cantidad posible de métodos de detección.
Respecto al caso particular de este trabajo, vale la pena remarcar
que los resultados obtenidos no dependen de la veracidad de las
ecuaciones (3,4) de la Introducción, pues se supuso que la
partícula móvil solo tiene masa y carga eléctrica y que
el monopolo magnético se encuentra fijo, por lo cual la
interacción electromagnética de la partícula móvil con
el campo magnético (cuyo origen no importa) está descrita por
la fórmula de Lorentz común (ec. (2), Introducción, la cual
es, como diría un publicista, de comprobada eficacia. El
procedimiento pierde esta base de veracidad fundamental si se
supone algún monopolo magnético móvil, pues su ecuación de
movimiento involucra entonces la fuerza de Lorentz generalizada
(ec. (4), Introducción).
Un dato un poco curioso sobre la aparente escasez (o no existencia)
de monopolos magnéticos se relaciona con la teoría de la
radiación cósmica de Fermi [78]. De acuerdo con ésta,
los rayos cósmicos adquieren sus elevadas energías de
campos magnéticos galácticos. De existir monopolos en
suficiente abundancia (y estando sujetos a la fuerza de Lorentz
generalizada de la ecuación (4) de la Introducción),
neutralizarían con el tiempo todos estos campos galácticos
(de la misma manera que las partículas eléctricas
neutralizan los campos eléctricos que aparecen en diversas zonas
de la galaxia), dejando así de producirse los rayos
cósmicos. De acuerdo con ésto puede pensarse que, si la
teoría de Fermi es correcta, los monopolos magnéticos deben
ser escasos no solamente en una vecindad de la tierra, sino en
toda nuestra galaxia. también, de acuerdo con lo mencionado en
la conclusión (5), un monopolo acelerado en los campos antes
mencionados, adquiriría una energía mucho más elevada
que las que adquieren las partículas eléctricas (rayos
cósmicos) que detectamos. La escasez de monopolos antes referida
tendría entonces relación con la no observación de ellos
en los rayos cósmicos, los cuales constituyen una fuente posible
para ellos.
2.
Con respecto al método especial empleado para determinar el grupo
de simetría clásico del problema, se puede tener la idea de
que es demasiado largo y tedioso, debido a lo cual no se
justificaría (aunque la comprobación directa de que las
componentes, de 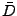 y
y 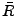 (ecs. (123,171), sección
I.C) son generadores del grupo de simetría en un ejercicio
algebraico también bastante largo). Sin embargo, se tiene en
favor de su uso que es un método sistemático en cuanto a que
sólo depende de la forma funcional del Hamiltoniano respecto a
las variables de acción [28]. En lo concerniente a la
consideración que se hizo de
(ecs. (123,171), sección
I.C) son generadores del grupo de simetría en un ejercicio
algebraico también bastante largo). Sin embargo, se tiene en
favor de su uso que es un método sistemático en cuanto a que
sólo depende de la forma funcional del Hamiltoniano respecto a
las variables de acción [28]. En lo concerniente a la
consideración que se hizo de 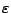 su ``variable
canónica conjugada" como nuevos grados de libertad (nuevas
dimensiones del espacio fase) para, al final, tomar como una
restricción su constancia, sin usar multiplicadores de Lagrange
en el proceso de solución del problema, es claro que ésto es
análogo a tener un problema de máximos y mínimos (las
ecuaciones de la Mecánica se obtienen de un principio
variacional, el de Hamilton), con restricciones, en el cual se
usan estas últimas hasta el final, sin emplear el método de
Lagrange. El mérito del procedimiento seguido con-siste en que
se evitó el formalismo un poco tedioso (cuado se trabaja con
varias dimensiones) de Lagrange y en que se obtiene un poco de
libertad (desde el punto de vista psicológico) para tratar como
parámetros lo que para la mayoría de las personas son
sólo constantes, con lo cual se está un poco mejor preparado
con respecto a cambios de puntos de vista en lo que se refiere a
la verdadera condición de lo que comúnmente se considera como
constantes (ejemplos, el concepto clásico de masa, el método
de obtener al límite clásico en Mecánica Cuántica
haciendo tender formalmente la constante de Planck a 0; el
procedimiento para obtener el límite no relativista haciendo
tender formalmente, en las fórmulas relativistas, la velocidad
de la luz a infinito, etc).
su ``variable
canónica conjugada" como nuevos grados de libertad (nuevas
dimensiones del espacio fase) para, al final, tomar como una
restricción su constancia, sin usar multiplicadores de Lagrange
en el proceso de solución del problema, es claro que ésto es
análogo a tener un problema de máximos y mínimos (las
ecuaciones de la Mecánica se obtienen de un principio
variacional, el de Hamilton), con restricciones, en el cual se
usan estas últimas hasta el final, sin emplear el método de
Lagrange. El mérito del procedimiento seguido con-siste en que
se evitó el formalismo un poco tedioso (cuado se trabaja con
varias dimensiones) de Lagrange y en que se obtiene un poco de
libertad (desde el punto de vista psicológico) para tratar como
parámetros lo que para la mayoría de las personas son
sólo constantes, con lo cual se está un poco mejor preparado
con respecto a cambios de puntos de vista en lo que se refiere a
la verdadera condición de lo que comúnmente se considera como
constantes (ejemplos, el concepto clásico de masa, el método
de obtener al límite clásico en Mecánica Cuántica
haciendo tender formalmente la constante de Planck a 0; el
procedimiento para obtener el límite no relativista haciendo
tender formalmente, en las fórmulas relativistas, la velocidad
de la luz a infinito, etc).
3.
El procedimiento que se sigue usualmente en la obtención de un
grupo dinámico consiste (ver referencias en la sección I.D) en
definir arbitrariamente funciones de las variables y momenta
canónicos y comprobar después que cumplen relaciones de
paréntesis de Poisson (clásicamente) y de conmutación
(cuánticamente) correspondientes a las de los generadores de
un grupo de Lie, el cual es grupo dinámico del problema. En el
presente trabajo, se identifica un grupo dinámico para el
problema clásico de una manera distinta: del conjunto de
eigenfunciones (bajo paréntesis de Poisson) de 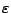 se
construyen productos (ecs. (101 - 108), sección I.C; ecs. (1-8),
sección I.D) que resultan ser los generadores de un grupo
dinámico; o sea, no tuvieron que definirse funciones con el
especial y único fin de construir los generadores del grupo
deseado. Me parece este método de trabajo más satisfactorio
que el primero citado y, observando que se basa, realmente, en la
consideración de
se
construyen productos (ecs. (101 - 108), sección I.C; ecs. (1-8),
sección I.D) que resultan ser los generadores de un grupo
dinámico; o sea, no tuvieron que definirse funciones con el
especial y único fin de construir los generadores del grupo
deseado. Me parece este método de trabajo más satisfactorio
que el primero citado y, observando que se basa, realmente, en la
consideración de 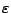 como una variable canónica
más, se puede conjeturar que sea ésta una manera
fructífera de trabajar, aunque la comprobación de ésto
tiene que hacerse aplicándola a más problemas y viendo si los
resultados obtenidos corroboran la certeza de la suposición.
como una variable canónica
más, se puede conjeturar que sea ésta una manera
fructífera de trabajar, aunque la comprobación de ésto
tiene que hacerse aplicándola a más problemas y viendo si los
resultados obtenidos corroboran la certeza de la suposición.
4.
Un resultado, estudiado en este trabajo, que es el que considero
el más interesante, es el referente a la cuantización de la
cantidad
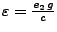 . Es sencillo verificar
que este resultado, junto con la evidencia experimental de que
existe una carga eléctrica de magnitud mínima (la carga
electrónica), implica la cuantización de la carga eléctrica
y de la magnética. La comprobación es la siguiente:
supongamos que
. Es sencillo verificar
que este resultado, junto con la evidencia experimental de que
existe una carga eléctrica de magnitud mínima (la carga
electrónica), implica la cuantización de la carga eléctrica
y de la magnética. La comprobación es la siguiente:
supongamos que
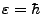 y que
y que 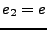 , siendo
, siendo 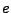 la carga electrónica (estas hipótesis son usados tan solo por
concretez; si se usa
la carga electrónica (estas hipótesis son usados tan solo por
concretez; si se usa
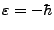 o la cuantización
obtenida al usar
o la cuantización
obtenida al usar  en la sección II.C, en cuyo
caso habría que tomar
en la sección II.C, en cuyo
caso habría que tomar
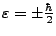 ,
los resultados obtenidos son identicos ), entonces g será igual,
en magnitud, a la cantidad mínima de carga magnética que se
puede tener en la naturaleza; llamamos
,
los resultados obtenidos son identicos ), entonces g será igual,
en magnitud, a la cantidad mínima de carga magnética que se
puede tener en la naturaleza; llamamos 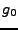 a este cuanto de
carga magnética. Supongamos ahora que colocamos en el campo del
monopolo con carga
a este cuanto de
carga magnética. Supongamos ahora que colocamos en el campo del
monopolo con carga 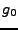 una partícula cargada
eléctricamente. Segun lo demostrado en la sección II.C, sólo
será posible físicamente este sistema dinámico para
una partícula cargada
eléctricamente. Segun lo demostrado en la sección II.C, sólo
será posible físicamente este sistema dinámico para
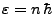 , con
, con 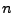 un entero; pero, para
un entero; pero, para 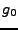 fijo, ésto se cumple si y sólo si la carga eléctrica de la
partícula es igual a
fijo, ésto se cumple si y sólo si la carga eléctrica de la
partícula es igual a 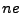 . Supongamos ahora que tenemos fija
una partícula con carga eléctrica
. Supongamos ahora que tenemos fija
una partícula con carga eléctrica 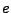 y que traemos a su
campo un monopolo magnético con carga magnética
y que traemos a su
campo un monopolo magnético con carga magnética 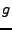 ;
Dirac [6] trató entre problema y encontro que también en
este caso se implica la condición de cuantización de
;
Dirac [6] trató entre problema y encontro que también en
este caso se implica la condición de cuantización de
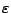 . Para el caso físicamente aceptable de tener
que
. Para el caso físicamente aceptable de tener
que 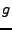 es tal que
es tal que
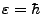 , se tendrá que
, se tendrá que  . Si ahora traemos un monopolo con carga
. Si ahora traemos un monopolo con carga 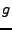 arbitraria, ya
que la carga eléctrica es fija (e), la condición
arbitraria, ya
que la carga eléctrica es fija (e), la condición
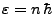 implica que
implica que  .
.
Respecto a la cuantización de 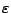 , hay un hecho que
considero importante, el cual es para mí bastante obscuro.
Como se demostró en la sección II.C, al usar dos potenciales
vectoriales"
, hay un hecho que
considero importante, el cual es para mí bastante obscuro.
Como se demostró en la sección II.C, al usar dos potenciales
vectoriales"  y
y  que dan el mismo campo
magnético
que dan el mismo campo
magnético  (o sea, que difieren tan sólo en una norma,
de acuerdo con las ecs. (13,20,21) de la Introducción), se
obtienen diferentes cuantizaciones para
(o sea, que difieren tan sólo en una norma,
de acuerdo con las ecs. (13,20,21) de la Introducción), se
obtienen diferentes cuantizaciones para 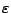 . La
diferencia entre éstas es fundamental; pues implica que los
cuantos de carga magnética
. La
diferencia entre éstas es fundamental; pues implica que los
cuantos de carga magnética 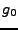 serán distintos en los dos
casos: en uno de ellos (usando
serán distintos en los dos
casos: en uno de ellos (usando  ) será doble que en el
otro (usando
) será doble que en el
otro (usando  ), pues existe sólo un cuanto de
electricidad. El efecto de las transformaciones de norma sobre las
eigenfunciones del Hamiltoniano es bien conocido y fácil de
obtener [14], resultando ser irrelevante, en cuanto a la
localización (en este caso particular) de la partícula
móvil, pues añaden una fase en la función de onda
), pues existe sólo un cuanto de
electricidad. El efecto de las transformaciones de norma sobre las
eigenfunciones del Hamiltoniano es bien conocido y fácil de
obtener [14], resultando ser irrelevante, en cuanto a la
localización (en este caso particular) de la partícula
móvil, pues añaden una fase en la función de onda 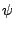 , la
cual desaparece el considerar el producto
, la
cual desaparece el considerar el producto  , que es
el que tiene significado físico. Sin embargo, el efecto, en
lo que se refiere al cálculo de valores de expectación de
operadores tales que no tienen a las funciones de onda como
eigenfunciones (o sea, que no representan constantes del
movimiento) no ha sido estudiado en forma adecuada. Además, el
efecto exacto de la inclusión de funciones de norma en la
definición de los operadores cuánticos tampoco ha sido
estudiado, hasta donde yo conozco el tema.
, que es
el que tiene significado físico. Sin embargo, el efecto, en
lo que se refiere al cálculo de valores de expectación de
operadores tales que no tienen a las funciones de onda como
eigenfunciones (o sea, que no representan constantes del
movimiento) no ha sido estudiado en forma adecuada. Además, el
efecto exacto de la inclusión de funciones de norma en la
definición de los operadores cuánticos tampoco ha sido
estudiado, hasta donde yo conozco el tema.
5.
Cuando se emprende un trabajo que implica algún tiempo (meses)
de ocupación, se debe tener idea, creo, de las causas que lo
motivan y de los fines perseguidos. Los comentarios a este
respecto, como es lógico, debí incluirlos al principio del
presente trabajo, pero, ya que los libros deben leerse en muchas
ocasiones del final al principio (invariablemente, el prólogo se
escribe al final), no creo faltar demasiado el orden lógico
incluyendo aquí los comentarios antes mencionados. Como
siempre que se dan argumentos sobre algo, se deben incluir dos
puntos de vista: el que se refiere al aspecto puramente personal y
el concerniente a la relación con el grupo humano del cual se
forma parte. Con respecto al interés personal por realizar el
presente trabajo, mencionaré el deseo de conocer, en forma
directa, algo sobre el movimiento esperado clásicamente en el
campo de una partícula hipotética, además de las
características exactas de la cuantización de una de las
propiedades fundamentales de dicha partícula (su carga
magnética) para que pueda dar lugar a un campo físicamente
aceptable, o sea, un campo tal que se obtengan estados del sistema
dinámico (monopolo electromagnético + partícula movil)
físicamente aceptables. El otro aspecto mencionado, el
referente a la relación que pueden tener los resultados
obtenidos con algún beneficio del grupo humano del cual formo
parte, es de discusión mucho más difícil. Aunque estoy
muy lejos de tener un punto de vista 100% utilitario (algunos
comentarios provechosos al respecto pueden verse en la
referencia (75)), mencionaré algunas razones, altamente
especulativas y descriptivas, por cierto, con el propósito de
demostrar que la motivación de este trabajo no fué 0%
utilitaria. Dichas razones dependen de utilizaciones que considero
posibles en México (tomando en cuenta su situación
tecnológica actual) de monopolos magnéticos, en caso de que
éstos existan:
i)
Pueden usarse como proyectiles en procesos de fisión de diversos
núcleos. Aunque esta utilización depende vitalmente de la
sección eficaz de los monopolos magnéticos en los varios
procesos involucrados, sobre la cuál no se tienen datos
teóricos, puede esperarse que ésta sea adecuadamente grande.
La ventaja esencial que se obtiene al usar monopolos magnéticos
en lugar de las partículas comúnmente empleados (protones,
neutrones, electrones) estriba en que los monopolos son
partículas suficientemente raras (al menos en esta parte del
universo), que pueden, por lo tanto, recobrarse después de
usadas [9], ya que no se pierden en un ambiente de
partículas idénticas. Se les puede recuperar, por ejemplo,
rodeando el ambiente del experimento de fisión con un material
ferromagnético, en el cual quedan absorbidos los monopolos,
sujetos a las fuerzas magnéticas dentro del material, pues
producen un agregado de dipolos magnéticos dentro del cual
quedan atrapados. Para recuperarlos, se puede calentar la
substancia ferromagnética usada y volverlos así a emplear una
y otra vez. Además, debido a que el cuanto de carga magnética
es aproximadamente 137 veces mayor que el correspondiente
eléctrico (ecs. (2,46) sección II.C), de acuerdo con la ec.
(4) de la Introducción (fuerza de Lorentz generalizada), las
interacciones del cuanto magnético con campos eléctricos y
magnéticos son aproximadamente 137 veces más fuertes que las
análogas de partículas eléctricas, debido a lo cual los
aceleradores de monopolos magnéticos pueden construirse de
dimensiones correspondientemente menores, siendo, entonces, más
baratos que los gigantes actuales para partículas
eléctricas, teniéndose energías comparables de los
proyectiles producidos (existe la alternativa, claro, de obtener
proyectiles magnéticos con energías fantásticamente
elevadas comparadas con las usuales, construyendo aceleradores de
dimensiones apropiadas).
ii)
Debido a la gran masa que (de existir) tienen los monopolos pues
se han hecho experimentos que indican [9] que dicha masa
debe ser mayor que el triple de la del protón, se les puede
emplear en la construcción de una versión ``magnética" del
microscopio iónico [76], con la ventaja de obtener, de
acuerdo con la fórmula DeBroglie para la longitud de onda
asociada
 , valores del momentum
, valores del momentum  mayores que los usuales y, por consiguiente, longitudes de onda
menores, aumentando así el poder de resolución. El uso
inmediato de tal aparato sería en el estudio de la estructura
de materiales. En Cristalografía podrían emplearse
también monopolos en arreglos de difracción. En cada caso,
existe la ventaja adicional de poder recuperar los monopolos
empleados. Hay que aclarar que los problemas de enfoque son
no-triviales [77].
mayores que los usuales y, por consiguiente, longitudes de onda
menores, aumentando así el poder de resolución. El uso
inmediato de tal aparato sería en el estudio de la estructura
de materiales. En Cristalografía podrían emplearse
también monopolos en arreglos de difracción. En cada caso,
existe la ventaja adicional de poder recuperar los monopolos
empleados. Hay que aclarar que los problemas de enfoque son
no-triviales [77].
Podría seguirse especulando de esta manera puramente descriptiva,
extendiéndose demasiado la lista; sin embargo, considero las dos aplicaciones
posibles mencionadas suficientemente generales.



Next: Bibliograf´ia
Up: INSTITUTO POLITÉCNICO NACIONAL ESCUELA
Previous: Grupo de simetría cuántico
Contents
José Pedro Hernández Enríquez
2006-12-10