Índice

• Tratamiento clásico del problema del movimiento de una partícula cargada eléctricamente en el campo de un monopolo eléctrico y magnético fijo
  • Resumen
  • Características generales del movimiento en el campo de un monopolo magnético
  • Tratamiento Hamiltoniano del problema
  • Determinación de un grupo dinámico clásico del problema, para estados ligados
  
  
• Tratamiento cuántico del problema
  • Resumen
  • Ecuación de Schrödinger para el problema
  • Cuantización de y de la componente del momento angular
  • Grupo de simetría cuántico del problema
  
  
• Conclusiones
• Bibliograf´ia

P R Ó L O G O

Como se desprende de su título, el objeto del presente trabajo es el estudio de las características esenciales del movimiento de una partícula con carga eléctrica en el campo de un monopolo eléctrico y magnético fijo. Incluye este estudio el tratamiento clásico y cuántico (basado este último en la ecuación de Schrödinger) del problema; estando el énfasis en: a) un método de determinación de los grupos clásicos de simetría y dinámico del mismo, el cual es de aplicabilidad siempre que el Hamiltoniano del sistema sea función sólo de la suma de las coordenadas de acción; b) el proceso de cuantización de la carga magnética; c) el uso de coordenadas cuadrático parabólicas. Comprende esta tesis una Introducción (en la cual se anotan y discuten los fundamentos sobre los cuales se basa la herramienta de Electromagnetismo que se usa) y los tres capítulos siguientes:

I.-

Tratamiento clásico. Se estudian en él las características generales del movimiento en el campo de un monopolo magnético (sección I-B); se determina el grupo de simetría (sección I-C) y un grupo dinámico (sección I-D) para estados acotados, o sea, estados de energía total $E<O$, pues los generadores empleados dependen todos de esta condición.

II.-

Tratamiento cuántico.- Se trabaja en el esquema de Schrödinger y se obtiene la fórmula para la energía (sección II-B). Se obtiene la cuantización de la carga magnética (sección II-C) y el grupo de simetría (sección II-D).

III.-

Conclusiones: Se incluyen las que considero más relevantes.

En cuanto a la notación: las coordenadas esféricas se denotan por $\rho, \theta, \phi$; la notación para el paréntesis de Poisson y el conmutador cuántico de dos cantidades $A$ y $B$ es la misma: $[A, B]$ , pues no hay peligro de confusión. La numeración de las fórmulas, tablas y figuras es independiente para cada seccción. En el Texto, las referencias a fórmulas se anotan con números entre paréntesis al nivel del renglón y las correspondientes a la Bibliografía con números entre paréntesis encima del renglón.

Respecto al proceso de desarrollo de esta tesis, deseo expresar mi agradecimiento al Profesor Harold V. McIntosh por haberme introducido al tema y por las provechosas discusiones que hemos tenido. También, va mi reconoci- miento a la Escuela Superior de Física y Matemáticas por las facilidades con que he contado para el desarrollo de mi trabajo en la misma; hago extensivo este reconocimiento a mis Profesores (de ayer y de hoy) y a todas aquellas personas que directa o indirectamente han contribuído a la realización de este trabajo por medio de su influencia en mi formación no sólo académica.

I N T R O D U C C I Ó N

El problema del monopolo magnético tiene una historia que puede considerarse ya como larga. El trabajo importante más antiguo sobre él es el de Poincaré [1] de 1896, en el cual estudia las órbitas resultantes en el movimiento de un electrón en el campo de un monopolo eléctrico y magnético; también en este trabajo, identifica e interpreta geométricamente las constantes del movimiento.

La causa más importante de que se haya especulado sobre la existencia de monopolos magnéticos, consiste en que no hay nada en la teoría Maxwelliana del Electromagnetismo cuya consistencia se pierda si existen: se puede elaborar una teoría electromagnética perfectamente consistente y que tome en cuenta la existencia de monopolos eléctricos y magnéticos. Esta teoría como se verá después, se basa en un conjunto de ecuaciones: desde este punto de vista, puede decirse que si ``hay lugar" en la teoría Electromagnética clásica para los monopolos magnéticos.

Además, las ecuaciones de la teoría resultante son notablemente más simétricos que las originales de Maxwell, y siempre ha satisfecho más el intelecto humano el conocimiento de estructuras de alguna manera simétricas, que el de estructuras sin simetrías aparentes [2], debido a la belleza intrínseca de las primeras. También, es bien conocido que las simetrías, en Física, implican leyes de conservación, siendo éstas las de aplicación más general y las que dan las bases para entender los fenómenos físicos [3]. Se sabe [4] que el hecho de no poder distinguir (por medio de mediciones de sus observables) entre dos situaciones de un sistema físico dado, implica la no conservación de alguna o algunas cantidades (observables) del mismo, y que el hecho contrario implica la no conservación de observables relacionadas. En el caso del Electromagnetismo, el tener el campo eléctrico como fundamentalmente distinto del campo magnético (ausencia aparente de monopolos magnéticos) implica la no conservación de alguna cantidad, el conocimiento de cuya constancia en el caso de que los campos eléctricos y magnético aparecieran simétricamente en las ecuaciones de Maxwell sería tal vez de gran utilidad en el entendimiento de la naturaleza de estos campos.

Las ecuaciones de Maxwell en ausencia de medios materiales son:

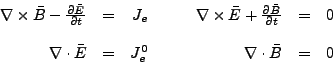$$\begin{array}{rrrrrrrr} \nabla \times \bar{B} - \frac{\par... ...E} & = &J_e^0 & & & \nabla \cdot \bar{B} & = & 0 \end{array}$$ (1)

La fuerza de Lorents está dada por:

$$\bar{F} = J_e^0 \;\bar{E} + \bar{J}_e \times \bar{B}$$ (2)

Las ecuaciones que generalizan a las anteriores al tomar en cuenta la existencia de monopolos magnéticos son las siguientes [5]:

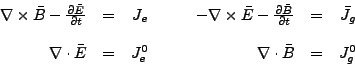$$\begin{array}{rrrrrrrr} \nabla \times \bar{B} - \frac{\par... ...= &J_e^0 & & & \nabla \cdot \bar{B} & = & J_g^0 \end{array}$$ (3)

Las fuerza de Lorentz generalizada está dada por:

$$\bar{F} = J_e^0 \;\bar{E} + \bar{J_e} \times \bar{B} + J_g^0\; \bar{B} - \bar{J_g} \times \bar{E}$$ (4)

En las ecuaciones anteriores, $J_e^0$ y $J_e = J_e^0 \;\bar{v}$ son las densidades de carga y corriente eléctricas, respectivamente, siendo $\bar{v}$ la velocidad de la carga eléctrica (o, en general, del elemento de volumen con densidad de carga $J_e^0$) que da lugar a $\bar{J_e} \cdot J_g^0$ y $J_g = J_g^0\; \bar{v}$ son las correspondientes densidades de carga y corriente magnéticas, respectivamente.

Es importante notar que la única base que se tiene para hacer las generalizaciones (3,4) consiste en razones de simetría. Se volverá a este punto en la conclusiones del presente trabajo.

Las ecuaciones anteriores no están referidas a ningún sistema de unidades particular. Ya que se trabajará con unidades C.G.S. se incluirán las ecuaciones (3) y (4) en estas unidades, pues, como representan tan sólo generalizaciones de (1,2), no es obvia (ni única) la manera en que deben introducirse las constantes $c$ y $4\pi$ que se tienen para las ecuaciones de Maxwell en unidades Gaussianas [5]:

$$\begin{array}{rrrrrrrr} \nabla \times \bar{B} - \frac 1 c ... ...t \bar{B} & = & 4\pi J_g^0 \end{array} \eqno{(3\mbox{-a})}$$

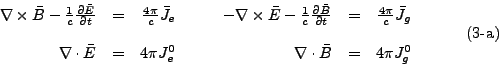
La fuerza de Lorentz sobre una partícula con carga eléctrica $J_e^0 = e_2$ y magnética $J_g^0 = g_2$, moviéndose con velocidad $\bar{v}$ en una región donde existen campos eléctrico $\bar{E}$ y magnético $\bar{B}$ está dada por [5]:

$$\bar{F} = e_2(\bar{E} + \frac{1}{c} \;\bar{v} \times \bar{... ... - \frac{1}{c} \;\bar{v} \times \bar{E}) \eqno{(4\mbox{-a})}$$

Con respecto a la no existencia aparente hasta hoy de monopolos magné- ticos, es pertinente hacer notar lo siguiente: las ecuaciones (3,4) son invariantes bajo la transformación [5]:

$$\bar{E}\to \bar{E}_1 , \quad \bar{B}\to \bar{B}_1 , \quad J... ..._{e1} , \quad J_g^\mu \to J^\mu_{g1} , \quad \mbox{tal que:}$$

$$\left. \begin{array}{ccc} \bar{E} & = & \cos \theta \ba... ..., J^\mu_{e1} + \cos\theta J^\mu_{g1} \end{array} \right\}$$ (5)

En lo anterior, $\theta$ es un ángulo arbitrario; $\mu = 0,1,2,3,4.$

Pero las ecuaciones (1,2) se obtienen de las (3,4) por medio de una transformación del tipo (5), si suponemos que toda partícula cargada tiene carga eléctrica y magnética, de tal manera que $J^\mu_{g_1} = \alpha J^\mu_{e_1}$, con $\alpha$ una cantidad dada por:

$$\alpha = -\tan \theta$$ (6)

Por lo tanto, si se cumple lo anterior, se puede tener un universo en el cual existen cargas magnéticas, descrito por las ecuaciones de Maxwell usadas comúnmente (1,2), o sea, en el cual no pueden detectarse (ó, de otra manera, se detectan cada vez que se detectan cargas eléctricas, de acuerdo con (6)). Sin embargo, no son claras las implicaciones del resultado anterior, (que puede ser fundamental), pues el ángulo $\theta$ es arbitrario, por lo que $\tan\theta \in (-\infty, \infty)$: según ésto, para cualquier valor que pueda tener $J^0_g$ en la naturaleza (en una partícula), se puede hallar un ángulo $\theta$ tal que la carga eléctrica $J^0_{e_1}$ asociada a la partícula está dada por $J^0_e = -\csc\theta J^0_{g_1}$, con $\alpha = -\tan\theta$. Esto implica que $J^\mu_e = \frac{1}{\alpha} \sqrt{\alpha^{2}{-1}}\; J^\mu_{g_1}$; o sea, se puede dar una descripción de tal sistema usando las ecuaciones de Maxwell (1,2) ordinarias. O sea, desde el punto de vista puramente Electromagnético, de acuerdo con lo anterior, aunque existieran partículas magnéticamente cargadas, no podrían detectarse (siendo $J^0_{g_1}$ su carga magnética, se detectarían como partículas con carga eléctrica $J^0_e = \frac{1}{\alpha} \sqrt{\alpha^{2}{-1}}\; J^0_{g_1}$, con $\alpha = -\tan\theta$, para algún valor de $\theta$ no determinado por los argumentos anteriores).

La literatura sobre el problema de monopolo magnético aumentó conside-rablemente a partir del trabajo de Dirac [6] sobre las restricciones cuánticas para la existencia del mismo. Los trabajos son de dos tipos principales: del primer tipo, son aquellos en los cuales se trata de dar una fundamentación teórica a la existencia o inexistencia de monopolos magnéticos (referencias 5,6,7,12), incluyendo su proposición como constituyentes de partículas elementales [18], del segundo tipo, son aquellos sobre intentos de tipo experimental para detectar monopolos magnéticos [9], la referencia [9] contiene una lista de trabajos sobre el último tipo de problema. Es particularmente interesante el método empleado en el primer trabajo de la ref. [9], se trató de determinar la existencia de monopolos magnéticos en las muestras lunares traídas a la tierra por la nave Apolo 11, en 1969, por medio del campo eléctrico que producen (el que se espera que debe producir, si las ecuaciones (3) son correctas) cuando están en movimiento. La luna es un lugar muy apropiado para buscar monopolos magnéticos si se supone que éstos forman parte también de los rayos cósmicos o que son producidos por otras partículas de éstos al tener colisiones con átomos de la superficie lunar, pues en ella prácticamente no hay erosión y, además, no tiene campo magnético (o es muy débil), el cual interferiría en el movimiento de estas partículas en el caso de que se acercaron a la tierra. Los resultados obtenidos fueron, como en el caso de los demás reportes al respecto, negativos.

En lo que sigue, se darán algunas consideraciones generales sobre el potencial del cual se obtiene el campo (supuesto) de un monopolo magnético, las cuales son de consecuencia en el desarrollo del problema.

El campo de fuerza de un monopolo magnético es muy parecido al de uno eléctrico, estando descrito por la expresión:

$$\bar{B} = K \frac{g}{p^2}\widehat{p}$$ (9)

La expresión anterior se obtiene de la última de las ecs. (3) y de la ec. (4), por un procedimiento análogo al de la obtención de la Ley de Coulomb a partir de la de Gauss. Se anotan algunos comentarios sobre este campo $\bar{B}$ en el capítulo de Conclusiones.

En la expresión (9), $\bar{p}$ es un vector de la posición del monopolo a la del punto de observación, $p$ es su magnitud y $\widehat{p}=\frac {\bar{p}} p$; $g$ es la carga magnética del monopolo y $k$ es una constante que depende de las unidades empleadas (puede hacerse igual a 1 escogiendo las unidades para $g$ tales que la fuerza entre dos monopolos magnéticos unitarios, sea unitaria a la distancia unidad, como en el caso de unidades eléctricas C.G.S.). Es claro que, si el monopolo es puntual, $\bar{\nabla} \cdot \bar{B} = 0$ en todo el espacio excepto en el punto donde se encuentra dicho monopolo, por lo cual [10], existe un ``potencial vectorial'' $\bar{A}$ tal que:

$$\bar{B} = {\nabla} \times \bar{A}$$ (10)

para todo punto del espacio, excepto aquel en el cual se encuentra el monopolo. Esto da una restricción muy importante para el tratamiento clásico del problema (y también para el tratamiento cuántico, pues éste está íntimamente ligado con el clásico y depende, para su aplicación, de la misma circunstancia: la existencia de un potencial), pues el formulismo Hamiltoniano sólo se puede usar donde la ec. (10) es válida, debido a lo siguiente:

El tratamiento Hamiltoniano depende de que sean válidas las ecuaciones de Lagrange en su forma:

$$\frac{d}{dt} \left( \frac{\partial{\cal L}}{\partial q_\ell} \right) - \frac{\partial{\cal L}}{\partial q_\ell} = 0$$ (11)

O sea, se requiere que todas las fuerzas generalizadas $F_l$ que aparezcan sean derivables de un potencial $U$ tal que [11]:

$$F_\ell = -\frac{\partial U}{\partial q_\ell} + \frac{d}{dt} \left( \frac{\partial U}{\partial q_\ell} \right)$$ (12)

Para el caso en que se tienen fuerzas electromagnéticas, se demuestra [11] que la existencia de $U$ depende de que exista un ``potencial vectorial" $\bar{A}$ tal que el campo magnético $\bar{B}$ esté dado por la ecuación (10); como ésto es posible donde no se tienen cargas magnéticas (o sea, donde $\nabla \cdot \bar{B}=0$), se tiene que se puede aplicar el tratamiento Hamiltoniano al problema y que éste será válido en todo el espacio excepto en los puntos donde haya monopolos magnéticos. Si se tiene que $\nabla \cdot \bar{B}\ne 0 \;\; \; \forall \;\; \bar{p} \in {\cal M}$, con ${\cal M}$ un subconjunto denso de $\Re^3$, es claro que el tratamiento Hamiltoniano no será aplicable en todo el espacio. En términos más físicos, si existe una región del espacio tal que $\nabla \cdot \bar{B}\ne 0$ para puntos de esa región arbitrariamente cercanos, no se puede aplicar el tratamiento Hamiltoniano en ella.

El tratamento Hamiltoniano que se usa en la versión clásica de este trabajo, se justifica por el hecho de que sólo se considera un monopolo magnético, puntual, tomando el punto que ocupa como el origen del sistema coordenado. Como el monopolo se considera fijo, el tratamiento Hamiltoniano será válido para todo el espacio, excepto el origen.

El campo $\bar{B}$ de la ec.(9) se puede obtener, de acuerdo con la ec.(10) de cualquiera de los dos potenciales siguientes [12].

$$\bar{A} (\bar {p}) = g \frac {(\bar{p} \times \widehat... ...ot \widehat{n})} {p [p^2 - (\bar {p} \cdot \widehat {n})^2]}$$ (13)

$$\bar A_1 (\bar {p}) = g \frac {\bar {p} \times \widehat {n}} {p (p-\bar{p} \cdot \widehat {n})}$$ (14)

En las ecs. (13,14), $\widehat n$ es un vector unitario arbitrario constante; o, sea los potenciales $\bar A$ , $\bar A_1$, no están completamente determinados, pues podemos escoger cualquier dirección $\widehat n$; esto sugiere que el campo que se obtenga de $\bar A$ o $\bar A_1$ será simétrico con respecto a rotaciones. Que esto último es cierto es evidente de la ec (9).

Ya que los ``potenciales" (13,14) dan lugar al mismo campo, o sea, tienen el mismo rotacional, deben diferir a lo más en una función $\bar f_1 (\bar {p} , \widehat {n})$, tal que existe una función $f (\bar{p} , \widehat{n})$ que cumple:

$$\bar{A} = \bar A_1 + \bar f_1 (\bar p , \widehat n) = \bar A_1 + \nabla [ f (\bar p , \widehat n ) ]$$ (15)

Para obtener la función $f$, se puede trabajar con $\bar A$ y $\bar A_1$ en sus formas (13,14). Sin embargo, el procedimiento resulta muy largo. Se ahorra trabajo de la manera siguiente: dada la dirección $\widehat n$ que aparece en $\bar A$ y $\bar A_1$ (obviamente, debe ser la misma para ambos, pues queremos relacionarlos), podemos escoger, sin pérdida de generalidad, nuestro sistema coordenado de tal manera que uno de los ejes, digamos el $z$, coincida en dirección y sentido con $\widehat n$ . En este sistema coordenado (que se llamará $[x,y,z]$) se tiene que $\bar A$ y $\bar A_1$ toman la forma:

$$\bar A = \frac {gz} {p(x^2 + y^2)} (y, -x, 0)$$ (16)

$$\bar A_1 = \frac {g} {p (p-z)} (y, -x, 0)$$ (17)

Es directo demostrar, entonces, que:

$$\bar A = \bar A_1 + \nabla (+ g \phi)$$ (18)

Con $\phi = arc \tan \frac {y} {x}$. Para cualquier otro sistema coordenado $[x', y', z']$, podemos, entonces, considerar las ecuaciones de transformación $x = x (x', y', z')$, $y=y(x', y', z')$, $z=z (x', y', z')$, con lo cual tendremos que:

$$\bar A (x,' y,' z') = \bar A_1 (x', y', z') + \nabla ( g \phi)$$ (19)

$$\mbox{Con:} \qquad \phi (x', y', z') = arc \tan \frac {y(x', y', z')} {x( x', y', z')}$$

$\bar A$ y $\bar A_1$ que aparecen en (19) no son, claro, en general, las mismas relaciones funcionales que aparecen en (16, 17), pero la ecuación (19) es la misma que (18). Esto demuestra que no se pierde generalidad con la elección del sistema coordenado $[x,y,z]$.

En este trabajo, se usará el potencial $\bar A$ dado por (16). Es claro que, para cada norma (gauge) f, se obtendrá un potencial distinto. El hecho de usar $\bar A$ obedece a que el Hamiltoniano del problema toma una forma muy simétrica cuando se emplea (ec.(17), sección I-C). Este potencial ha sido usado más recientemente [8], pues en los primeros trabajos se usó invariablemente el empleado por Dirac [6] en su trabajo de 1931:

$$\bar A_2 = \frac {g} {p(p + z)} (-y, x,0)$$ (20)

$\bar A_2$ se obtiene de (14) al considerar los ejes $X, Y, Z$ de tal manera que $\widehat n = (0,0,-1)$; está relacionado con $\bar A$ por la expresión:

$$\bar A_2 = \bar A + \nabla (g\phi)$$ (21)

Se sabe que el efecto de una transformación de norma se traduce en un cambio de fase de la función de onda de un sistema [14]. Sin embargo, como se verá en el tratamiento cuántico del problema, el efecto de una transformación de fase es profundo en lo que a la cuantización de la carga magnética se refiere. Usando $\bar A_2$, se obtiene una cuantización tal que $\frac {\varepsilon}{\hbar} = \frac {ge_2}{\hbar e}$ puede tomar valores enteros o semienteros; usando $\bar A$; se obtiene que $\frac{\varepsilon}{\hbar}$ sólo puede tomar valores enteros ($e_2$ es una carga eléctrica). Se volverá a este punto en las conclusiones de este trabajo.