



Next: Autómatas celulares en una
Up: Teoría de autómata celular
Previous: Teoría de autómata celular
Contents
Aunque el nombre de John von Neumann en la actualidad
es fuertemente asociado con las computadoras que tienen una
arquitectura de una sola UCP (Unidad Central de Procesamiento),
es necesario recordar que von Neumann también es uno de los
principales pioneros de la computación paralela.
A principios de 1942, J. Presper Eckert, John W. Mauchly y sus
asociados de la Escuela de Ingeniería Eléctrica Moore de la
Universidad de Pennsylvania comenzaron la construcción de una
computadora electrónica digital de ``alta velocidad" para
satisfacer las necesidades de las Fuerzas Armadas de los Estados
Unidos. Eckert y Mauchly llamaron a su máquina ``Electrical
Numerical Integrator And Calculator", la cual vino a ser conocida
públicamente simplemente como ENIAC en 1946.
En 1945, von Neumann inició un estudio analítico de
la computación y probó que una computadora podía tener
una estructura física fija y simple, a diferencia del
diseño original de la ENIAC, en el cual el sistema operativo y
los programas de aplicación estaban almacenados en unidades
separadas las cuales tenían que ser conectadas a la ENIAC
para poder realizar los cálculos, además, las conexiones
variaban de un programa a otro. Poco tiempo después de su
análisis, von Neumann formó un grupo de investigación
encabezado por él mismo, Howard Aiken y Norbert Wiener para
trabajar en problemas sobre computadoras, comunicaciones,
análisis de series de tiempo y los ``aspectos de comunicación
y control del sistema nervioso humano". El último tópico fue
incluido debido al gran interés de von Neumann en el trabajo
sobre redes neuronales realizado por McCulloch y Pitts en 1943
[49]. En 1946, von Neumann diseñó la EDVAC (Electronic
Discrete Variable Computer), la primer máquina con un programa
almacenado. En 1947, bajo la influencia de las ideas sobre
autómatas desarrolladas por Post y Turing (1936), von Neumann
comenzó estudios sobre la complejidad requerida para que un
dispositivo o sistema fuese auto-reproductivo. Estos estudios
también incluían el problema de organizar un sistema
básicamente desde componentes no confiables (un campo de estudio
que actualmente se conoce como ``computación tolerante a
fallas"). En un principio, von Neumann investigó un modelo
continuo de un autómata auto-reproductivo basado en ecuaciones
diferenciales parciales, pero cuando encontró dificultades para
proveer reglas rigurosas y explícitas e instrucciones
necesarias para poder llevarlo a la práctica y cuando se hizo
evidente que este autómata podría ser muy grande,
redireccionó sus esfuerzos hacia un modelo de
auto-reproducción utilizando un arreglo de elementos
computacionales (células). Tanto Burks (1970) como Goldstine
(1972) confirman que la idea de tal arreglo fue sugerida a von
Neumman por Stanislaw Ulam. A von Neumman le atrajo la idea de
utilizar paralelismo porque esto podría eventualmente
proporcionarle una mayor velocidad en las computaciones.
Desafortunadamente, su muerte prematura en 1957 no le permitió
alcanzar completamente sus metas. De esta manera, se puede decir
que a principios de los 1950's von Neumann concibió a los
autómatas celulares.
La construcción original de
von Neumann de un arreglo celular (autómata celular)
auto-reproductivo requería que cada célula de un espacio
celular representado por una cuadrícula bi-dimensional
soportara un conjunto de 29 estados. El arreglo por sí mismo
requería apro-ximadamente 200,000 células. Además, el
valor del estado en que se encuentra cada célula del arreglo
localizada en una posición 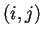 (donde
(donde 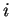 es la columna y
es la columna y
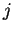 el renglón) en un tiempo
el renglón) en un tiempo 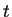 estará determinado por los
valores de los estados en que se encuentran las células
localizadas en las posiciones
estará determinado por los
valores de los estados en que se encuentran las células
localizadas en las posiciones 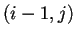 ,
, 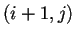 ,
, 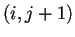 e
e
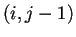 y el valor del estado en que se encuentra la célula
central localizada en la posición
y el valor del estado en que se encuentra la célula
central localizada en la posición 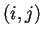 en el tiempo
en el tiempo 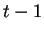 ;
cada célula del arreglo en algún momento será una célula
central, la cual junto con las células ubicadas arriba, abajo, a
la izquierda y a la derecha (ortogonalmente) de la misma forman lo
que se conoce como vecindad von Neumann (ver figura 3.1). Las
interacciones locales de las vecindades en un tiempo
;
cada célula del arreglo en algún momento será una célula
central, la cual junto con las células ubicadas arriba, abajo, a
la izquierda y a la derecha (ortogonalmente) de la misma forman lo
que se conoce como vecindad von Neumann (ver figura 3.1). Las
interacciones locales de las vecindades en un tiempo 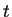 determinan el estado global del arreglo (el cual es actualizado
sincrónicamente) en el tiempo
determinan el estado global del arreglo (el cual es actualizado
sincrónicamente) en el tiempo 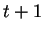 .
.
Figura 3.1:
Vecindad von Neumann.
|
|
Este grado de complejidad fue necesario debido a que von Neumann
buscaba diseñar su autómata como un sistema de computación
universal o máquina de Turing3.1. En los 1960's, E.F. Codd [19] propuso una
variante la cual requería ocho estados por célula y
seguía utilizando la vecindad von Neumann; otros
investigadores, en particular los del Instituto de Tecnología
de Massachusetts (M.I.T.) encontraron constructores
auto-reproductivos, aunque no universales de una naturaleza más
simple, en particular un autómata celular descubierto por
Fredkin [26], el cual era capaz de auto-reproducir
cualquier configuración inicial utilizando la vecindad von
Neumann y solamente dos estados por célula.
Ulam y Schrandt (1967) también investigaron
la dinámica de estos autómatas celulares de dos estados por
célula, y de hecho, extendieron su investigación estudiando
autómatas celulares en tres dimensiones. Su trabajo, junto con
el de investigadores tales como Tratcher, Moore, Myhill, Stein y
Holland son coleccionados en [13]. Subsecuentemente,
Banks [4] (un estudiante de Fredkin) probó la
existencia de un autómata celular tipo von Neumann
auto-reproductivo utilizando cuatro estados por célula.
Durante su investigación sobre autómatas celulares de
dos estados (en este caso 0 y 1), Ulam y Schrandt tenían
especial interés por los patrones formados por los grupos de
células en estado 0 y los grupos de células en estado 1 en
varias etapas durante las computaciones. Para ciertas reglas, una
configuración inicial de células en estado 1 ``sobre un fondo"
de células en estado 0 evolucionaba de tal forma que las
células en estado 1 se disipaban completamente, mientras que con
otras reglas el efecto era totalmente opuesto.
John
Conway, investigador interesado en encontrar una construcción
más simple que la de von Neumann, descubrió una regla para un
autómata celular de dos estados y un tipo de vecindad parecida a
la de von Neumann, con la variante de que se toma en cuenta a los
vecinos ubicados en las esquinas. A este tipo de vecindad se le
conoce como vecindad Moore (ver figura 3.2). Esta regla tenía
un efecto intermedio, es decir, llevaba eventualmente al
autómata ya sea a un patrón de comportamiento estable o a
patrones que exhibían algo repetitivo (por ejemplo, patrones
de comportamiento oscilatorios). Conway presentó en 1970 su
regla a la cual bautizó con el nombre ``Life".
Figura 3.2:
Vecindad Moore.
|
|
Life representa una especie de ``juego ecológico" ya que
las células del autómata pueden estar ``vivas" o ``muertas".
Life trabaja sobre una cuadrícula bi-dimensional
infinita y los estados de las células están determinados por
las siguientes condicionantes:
- NACIMIENTO. Una célula que está muerta en un
tiempo
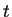 estará viva en un tiempo
estará viva en un tiempo 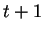 si y sólo si
exactamente tres de sus ocho vecinos están vivos en el tiempo
si y sólo si
exactamente tres de sus ocho vecinos están vivos en el tiempo
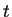 .
.
- MUERTE POR SOBRE-POBLACIÓN. Una célula que está viva en
un tiempo
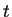 morirá en un tiempo
morirá en un tiempo 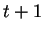 si cuatro o más de
sus ocho vecinos están vivos en el tiempo
si cuatro o más de
sus ocho vecinos están vivos en el tiempo 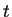 .
.
- MUERTE POR POCA POBLACIÓN (AISLAMIENTO). Una célula que está viva en
un tiempo
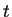 morirá en un tiempo
morirá en un tiempo 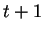 si a lo más uno de
sus ocho vecinos están vivos en el tiempo
si a lo más uno de
sus ocho vecinos están vivos en el tiempo 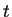 .
.
- SOBREVIVENCIA. Una célula que está viva en un
tiempo
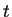 permanecerá viva en un tiempo
permanecerá viva en un tiempo 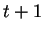 si dos o tres
de sus ocho vecinos están vivos en el tiempo
si dos o tres
de sus ocho vecinos están vivos en el tiempo 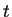 .
.
Life comienza a funcionar a partir de una configuración
inicial de células vivas sobre un fondo de células muertas.
Si se dan las condiciones, tanto los nacimientos como las muertes
de las células ocurrirán de manera simultánea y formarán
la configuración que constituirá una nueva generación
dentro de la evolución de Life.
Existen
configuraciones que permanecen estables durante toda la
evolución de Life. En el vocabulario de Life a
estas configuraciones se les conoce como ``still life". En
la figura 3.3, en la cual las células vivas se representan con
el color negro y las células muertas con el color blanco, se
pueden observar algunas configuraciones still life.
También existen configuraciones que desaparecen
después de transcurridas ciertas ge-neraciones. En la figura 3.4
se pueden observar algunas de estas configuraciones.
Uno de los descubrimientos de Conway más remarcable es
la figura formada por cinco células vivas llamada glider
(ver figura 3.5).
Figura 3.3:
A las configuraciones que permanecen estables durante toda la evolución del autómata celular se les conoce como still life.
|
|
Figura 3.4:
Configuraciones en las que todas la células vivas
mueren.
|
|
Como se oberva en la figura 3.5, después de
transcurridas dos generaciones, el glider tiene un ligero
acarreo hacia la derecha, el cual se ve reflejado en una
línea diagonal. A este fenómeno se le conoce como
``glide reflection" debido al nombre de la figura. Una vez que
transcurren dos generaciones más, el glider se endereza a
sí mismo y entonces se ha movido en la cuadrícula un
lugar diagonalmente hacia abajo y a la derecha desde su posición
inicial. Conway eligió el término velocidad de la luz
(haciendo una analogía del juego de ajedrez con respecto a la
velocidad a la que se desplaza el rey) para ilustrar que el
glider es el patrón que más rápido se mueve sobre la
cuadrícula. Ningún otro patrón puede reproducirse a
sí mismo lo bastante rápido como para moverse a tal
velocidad. De esta manera, Conway probó que la máxima
velocidad diagonalmente es un cuarto de la velocidad de la
luz ya que el glider se reproduce a sí mismo en la
misma orientación después de cuatro generaciones y ha viajado
un lugar diagonalmente en la cuadrícula. Por lo anterior, se
dice que un glider se desliza de un lado a otro del campo a
un cuarto de la velocidad de la luz.
Figura 3.5:
Uno de los descubrimientos de Conway más remarcable es
la figura formada por cinco células vivas llamada glider. Después de
transcurridas dos generaciones, el glider tiene un ligero
acarreo hacia la derecha, el cual se ve reflejado en una
línea diagonal. A este fenómeno se le conoce como ``glide reflection" debido al nombre de la figura. Una vez que
transcurren dos generaciones más, el glider se endereza a
sí mismo y entonces se ha movido en la cuadrícula un
lugar diagonalmente hacia abajo y a la derecha desde su posición
inicial.
|
|
``Life" se popularizó a partir de su publicación en la
columna mensual de Martin Gardner llamada ``Mathematical
Games" en Scientific American y posteriormente varias
personas presentaron resultados interesentes basados en sus
propias experimentaciones con ``Life". Aunque no de valor
práctico, ``Life" ha tenido el mayor impacto en la
investigación sobre autómatas celulares.
En la
década de los 1980's, los estudios de Stephen Wolfram sobre
autómatas celulares arrojaron resultados interesantes. Wolfram
realizó una investigación sobre las propiedades de los
autómatas celulares en una dimensión utilizando conceptos de
mecánica estadística y aprovechando que las
microcomputadoras, los lenguajes de programación, y los
monitores de video disponibles en ese momento eran lo
suficientemente capaces como para llevar a cabo un gran número
de estudios experimentales con autómatas celulares.
A diferencia de otros investigadores como Conway, por
ejemplo, el cual se concentró en una sola regla que sirviera
para sus propositos, Wolfram comparó un gran número de reglas
diferentes y posteriormente propuso una clasificación de acuerdo
a los diferentes patrones de comportamiento que había
observado.
Por otro lado, a pesar de que von Neumann
no pensó en los autómatas celulares como un objeto
matemático de estudio y aunque desde su surgimiento se les ha
utilizado en aplicaciones prácticas específicas como el
reconocimiento de patrones y el procesamiento de imágenes por citar algunas,
el estudio de los aspectos formales sobre el
comportamiento de los autómatas celulares también resulta muy
interesante. En este sentido, se han encontrado trabajos con
resultados aplicables al análisis teórico de los autómatas
celulares como los trabajos de Hedlund [30] y Birkhoff
[7] sobre sistemas dinámicos.




Next: Autómatas celulares en una
Up: Teoría de autómata celular
Previous: Teoría de autómata celular
Contents
rene
2003-10-20
![\includegraphics[width=2in]{3-1r}](img74.gif)
![\includegraphics[width=4in]{3-3r}](img76.gif)
![\includegraphics[width=4in]{3-5r}](img78.gif)