



Next: Función de transiciones locales
Up: Autómatas celulares en una
Previous: Autómatas celulares en una
Contents
Un autómata celular uni-dimensional consta de un
arreglo lineal finito de celdas o células (ver figura
3.6), una de las características por las cuales a los autómatas celulares en una
dimensión también se les conoce como Autómatas
Celulares Lineales. Cada célula del arreglo puede tomar como
valor un elemento de un conjunto finito de estados, el cual es
denotado por la letra 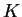 . Los elementos del conjunto
. Los elementos del conjunto 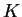 pueden
ser de diferentes tipos (números, letras, símbolos, etc.)
puesto que la naturaleza de los estados no es relevante. Para el
procesamiento interno de las evoluciones del autómata celular
lineal a través del tiempo lo más conveniente es utilizar
números, esto por cuestiones computacionales, y para la
representación final de esas evoluciones es útil utilizar
diferentes colores, esto por cuestiones de visualización. Aunque
la natulareza de los estados no influye en el comportamiento del
autómata celular lineal, la interacción que mantienen las
células durante la evolución por medio de esos estados sí
influye de manera directa en el comportamiento del autómata
celular lineal.
pueden
ser de diferentes tipos (números, letras, símbolos, etc.)
puesto que la naturaleza de los estados no es relevante. Para el
procesamiento interno de las evoluciones del autómata celular
lineal a través del tiempo lo más conveniente es utilizar
números, esto por cuestiones computacionales, y para la
representación final de esas evoluciones es útil utilizar
diferentes colores, esto por cuestiones de visualización. Aunque
la natulareza de los estados no influye en el comportamiento del
autómata celular lineal, la interacción que mantienen las
células durante la evolución por medio de esos estados sí
influye de manera directa en el comportamiento del autómata
celular lineal.
Figura 3.6:
Arreglo de 10 células.
|
|
El número de estados para un autómata celular lineal puede ser
variable, por esta razón en la notación Wolfram el número de
estados se representa por medio de la variable 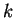 , es decir, la
cardinalidad del conjunto
, es decir, la
cardinalidad del conjunto 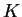 es igual a
es igual a 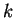 , lo cual se escribe
como
, lo cual se escribe
como 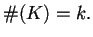
Otro elemento importante en la
notación Wolfram es el que él denomina como radio de
vecindad y que denota por medio de la variable 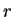 . El radio
de vecindad indica el rango de interacción a nivel local que
van a tener las células entre sí. Si
. El radio
de vecindad indica el rango de interacción a nivel local que
van a tener las células entre sí. Si 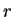 es igual a uno,
entonces cada célula del arreglo verá afectado su estado
durante la evolución del autómata a partir de los estados de
sus células vecinas más próximas tanto del lado izquierdo
como del lado derecho. Esto forma lo que se conoce como
vecindad, donde el tamaño total de una vecindad es igual a
es igual a uno,
entonces cada célula del arreglo verá afectado su estado
durante la evolución del autómata a partir de los estados de
sus células vecinas más próximas tanto del lado izquierdo
como del lado derecho. Esto forma lo que se conoce como
vecindad, donde el tamaño total de una vecindad es igual a 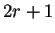 incluyendo a la célula central. Para el caso en el que
incluyendo a la célula central. Para el caso en el que 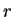 es igual a uno, el tamaño total de la vecindad va a ser igual a
tres (ver figura 3.7).
es igual a uno, el tamaño total de la vecindad va a ser igual a
tres (ver figura 3.7).
Figura 3.7:
Vecindad de tamaño tres.
|
|
Un punto importante a mencionar es que al ser finito el arreglo
la primera y la última célula no tendrán vecinos del lado
izquierdo y derecho respectivamente. Una manera de solucionar
esto es tomar el arreglo como un anillo, es decir, cerrando el
arreglo en forma circular para conservar la uniformidad en todas
las vecindades (ver figura 3.8), además, al tomar el arreglo
como un anillo se establecen los límites a la frontera o
condiciones de límites periódicos.
Figura 3.8:
Estructura de un autómata celular lineal estableciendo
condiciones de límites periódicos.
|
|




Next: Función de transiciones locales
Up: Autómatas celulares en una
Previous: Autómatas celulares en una
Contents
rene
2003-10-20
![\includegraphics[width=3.3in]{3-6r}](img80.gif)
![\includegraphics[width=4in]{3-8r}](img85.gif)