



Next: Clasificación de Wolfram
Up: Autómatas celulares en una
Previous: Función de transiciones locales
Contents
Como se mencionó en la sección 3.2.1., un
autómata celular uni-dimensional consta de un arreglo lineal
finito de células, es decir, existe una correspondencia
biunívoca entre el conjunto 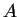 de células que forman el
arreglo y una sección
de células que forman el
arreglo y una sección 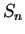 de los números naturales, donde
llamaremos una sección del conjunto
de los números naturales, donde
llamaremos una sección del conjunto 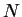 de los números
naturales denotada por
de los números
naturales denotada por 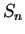 al conjunto de los primeros
al conjunto de los primeros 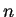 números naturales, esto es:
números naturales, esto es:
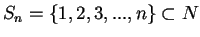 . Por lo tanto, decimos que
. Por lo tanto, decimos que 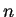 es la cardinalidad del conjunto
es la cardinalidad del conjunto
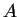 , es decir,
, es decir, 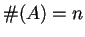 y de esta manera sabemos con certeza
que el conjunto
y de esta manera sabemos con certeza
que el conjunto 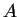 de células que forman el arreglo es un
conjunto finito. Este arreglo de células en un determinado
estado constituye una configuración global que conforma una
generación
de células que forman el arreglo es un
conjunto finito. Este arreglo de células en un determinado
estado constituye una configuración global que conforma una
generación 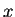 en una tiempo
en una tiempo 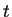 dentro de la evolución del
autómata. De esta forma se asume que todas las configuraciones
globales posibles que se pueden formar durante la evolución del
autómata celular lineal son finitas puesto que la longitud de
éstas tiene que ajustarse al tamaño del arreglo. Las
configuraciones globales que constituyen las generaciones que
surgen durante la evolución del autómata se forman a partir de
las transiciones locales, tal como se observa en la figura 3.12.
dentro de la evolución del
autómata. De esta forma se asume que todas las configuraciones
globales posibles que se pueden formar durante la evolución del
autómata celular lineal son finitas puesto que la longitud de
éstas tiene que ajustarse al tamaño del arreglo. Las
configuraciones globales que constituyen las generaciones que
surgen durante la evolución del autómata se forman a partir de
las transiciones locales, tal como se observa en la figura 3.12.
Dada la configuración global inicial que se muestra en la
figura 3.12, después de transcurridas 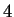 generaciones todas las
células del autómata convergen al estado
generaciones todas las
células del autómata convergen al estado 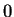 . Es importante
mencionar que la longitud del arreglo que constituye el autómata
es de solamente diez células. La razón por la cual se toma un
arreglo tan pequeño es el tratar de agilizar la comprensión de
los conceptos que se manejan en esta tesis. Es por eso que a lo
largo de la misma se utlizan arreglos de longitud pequeña cuando
se pretende explicar diversos aspectos que tienen que ver con la
teoría de autómata celular.
. Es importante
mencionar que la longitud del arreglo que constituye el autómata
es de solamente diez células. La razón por la cual se toma un
arreglo tan pequeño es el tratar de agilizar la comprensión de
los conceptos que se manejan en esta tesis. Es por eso que a lo
largo de la misma se utlizan arreglos de longitud pequeña cuando
se pretende explicar diversos aspectos que tienen que ver con la
teoría de autómata celular.
Figura 3.12:
Transiciones globales de un autómata celular lineal
(2,1) aplicando la regla 54.
|
|
El paso de una configuración global a otra, es decir, la
evolución del autómata de una generación a otra define la
función de transiciones globales
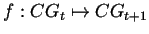 ,
donde el conjunto
,
donde el conjunto 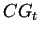 representa el estado global del
autómata en el tiempo
representa el estado global del
autómata en el tiempo 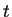 , y el conjunto
, y el conjunto 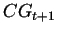 representa
el estado global del autómata en el tiempo
representa
el estado global del autómata en el tiempo 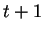 , es decir, en
la siguiente generación. En la figura 3.13 se ilustra la
función de transiciones globales tomando las configuraciones de
la figura 3.12, aunque en ésta se expresan en notación
decimal. Los elementos del conjunto
, es decir, en
la siguiente generación. En la figura 3.13 se ilustra la
función de transiciones globales tomando las configuraciones de
la figura 3.12, aunque en ésta se expresan en notación
decimal. Los elementos del conjunto 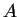 representan el dominio de
la función, esto es, los estados globales que se generan a
partir de la configuración inicial cuyo número decimal es 561
aplicando la regla 54 en un determinado tiempo
representan el dominio de
la función, esto es, los estados globales que se generan a
partir de la configuración inicial cuyo número decimal es 561
aplicando la regla 54 en un determinado tiempo 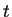 , y los
elementos del conjunto
, y los
elementos del conjunto 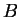 representan la imagen de la función,
esto es, los estados globales del autómata que se generan a
partir de un determinado tiempo
representan la imagen de la función,
esto es, los estados globales del autómata que se generan a
partir de un determinado tiempo 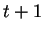 . Tanto el dominio
. Tanto el dominio 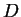 como
la imagen
como
la imagen 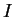 son subconjuntos de
son subconjuntos de 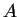 y
y 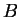 respectivamente es
decir,
respectivamente es
decir, 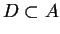 e
e 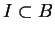 . Los conjuntos
. Los conjuntos 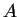 y
y 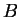 contienen tantos elementos como configuraciones distintas puedan
existir. En la figura 3.13 sólamente se incluyen los elementos que
definen la función para este caso en particular.
contienen tantos elementos como configuraciones distintas puedan
existir. En la figura 3.13 sólamente se incluyen los elementos que
definen la función para este caso en particular.
Figura 3.13:
Función de transiciones globales aplicando la regla
54.
|
|




Next: Clasificación de Wolfram
Up: Autómatas celulares en una
Previous: Función de transiciones locales
Contents
rene
2003-10-20
![\includegraphics[width=3.9in]{3-12r}](img101.gif)