



Next: Construcción de los diagramas
Up: Analizando el AC de
Previous: Regla equivalente con un
Contents
Se puede resumir que la regla 43 tiene limitaciones porque no incluye a todas las variables involucradas en el modelo de Nagel. Una manera de solucionar esto es que los diferentes valores que puede tomar 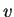 también los pueda tomar
también los pueda tomar 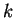 , es decir, que las velocidades de los autos sean estados que formen parte del autómata celular que reproduce el flujo de tránsito de autos.
, es decir, que las velocidades de los autos sean estados que formen parte del autómata celular que reproduce el flujo de tránsito de autos.
En esta sección se muestra un autómata celular que tiene un comportamiento equivalente al del modelo de Nagel con 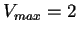 . A este autómata se le dió por nombre LCATRAFFICFLOWVMAX2. Este autómata pasa de ser de tipo (2,1) a tipo (4,2). Es de tipo (4,2) porque los estados que pueden tomar las células (sitios) son: vacío, ocupado por un auto con velocidad 0 (estacionado), ocupado por un auto con velocidad 1 y ocupado por un auto con velocidad 2.
. A este autómata se le dió por nombre LCATRAFFICFLOWVMAX2. Este autómata pasa de ser de tipo (2,1) a tipo (4,2). Es de tipo (4,2) porque los estados que pueden tomar las células (sitios) son: vacío, ocupado por un auto con velocidad 0 (estacionado), ocupado por un auto con velocidad 1 y ocupado por un auto con velocidad 2.
El radio de vecindad se extiende a 2 porque 2 es el número máximo de sitios que pueden avanzar los autos, de esta manera se contemplan todas las configuraciones locales que se pueden dar con 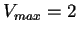 . Esta especie de monitoreo a los sitios es algo parecido a lo que se plantea en el modelo de Fuks y Boccara, con la diferencia de que el bloque de sitios que se revisa en este autómata es el mismo en ambas direcciones.
. Esta especie de monitoreo a los sitios es algo parecido a lo que se plantea en el modelo de Fuks y Boccara, con la diferencia de que el bloque de sitios que se revisa en este autómata es el mismo en ambas direcciones.
Es importante mencionar que para un autómata celular (4,2) el número total de vecindades es dado por 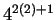 y el número total de reglas de evolución distintas es dado por
y el número total de reglas de evolución distintas es dado por
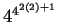 , esto muestra el incremento exponencial del autómata en cuanto a su complejidad y a la dificultad para analizarlo.
, esto muestra el incremento exponencial del autómata en cuanto a su complejidad y a la dificultad para analizarlo.
Por lo anterior, es muy complicado revisar todas las reglas para saber cual se ajusta a las características requeridas. Por esta razón se optó por llevar a cabo algo semejante a lo que se hizo para encontrar la regla de Autómata Celular (2,1) 43.
Para encontrar la regla con comportamiento equivalente al del modelo de Nagel lo que se hizo fue calcular las 1024 vecindades y posteriormente determinar el estado de evolución de cada una de las células centrales en base a la mecánica del modelo original.
En las siguientes figuras se muestran las vecindades y su respectivo estado de evolución (segunda y tercer columna de izquierda a derecha). Los elementos del conjunto de estados de este autómata son
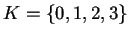 donde 0 representa un sitio vacío, 1 representa un sitio ocupado por un auto con velocidad 0, 2 un sitio ocupado por un auto con velocidad 1 y 3 un sitio ocupado por un auto con velocidad 2. La tercera columna constituye la regla de evolución del autómata.
donde 0 representa un sitio vacío, 1 representa un sitio ocupado por un auto con velocidad 0, 2 un sitio ocupado por un auto con velocidad 1 y 3 un sitio ocupado por un auto con velocidad 2. La tercera columna constituye la regla de evolución del autómata.
Figura 5.9:
Vecindades que conforman el autómata el cual tiene un comportamiento equi-valente al del modelo de Nagel con 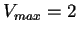 .
.
|
|
Figura 5.9:
Continuación...
|
|
Figura 5.9:
Continuación...
|
|
Figura 5.9:
Continuación...
|
|
Figura 5.9:
Continuación...
|
|
Figura 5.9:
Continuación...
|
|
Figura 5.9:
Continuación...
|
|
Figura 5.9:
Continuación...
|
|
Figura 5.9:
Continuación...
|
|
Figura 5.9:
Continuación...
|
|
Figura 5.9:
Continuación...
|
|
Subsections




Next: Construcción de los diagramas
Up: Analizando el AC de
Previous: Regla equivalente con un
Contents
rene
2003-10-20
![\includegraphics[width=5.5in]{5-9r}](img262.gif)
![\includegraphics[width=5.5in]{5-9r}](img262.gif)