Regla equivalente con un Autómata (2,1)

De acuerdo a lo anterior se utilizó igualmente un arreglo de 10 sitios y se estableció una configuración inicial para posteriormente iterarla aplicando los pasos del modelo de Nagel con la finalidad de encontrar una regla de autómata celular que reproduciese el comportamiento del modelo para tránsito de autos de Nagel.

Figura 5.4: Diagrama de Bruijn de la regla 43.

Tabla 5.1: Regla de AC(2,1) 43.

Vecindad	Estado al que evoluciona la célula central
000	1
001	1
010	0
011	1
100	0
101	1
110	0
111	0

Como se puede apreciar en la figura 5.3 se iteró el arreglo dando a 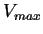$V_{max}$ un valor de 3 y a la densidad 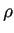$\rho$ un valor de 0.5. Como se puede observar, después de la onceava iteración se repite la secuencia generada a partir de la configuración inicial dando como resultado un ciclo que en términos de la teoría de autómata celular inicia a partir de la generación 1 y se cierra en la generación 10, es decir, es un ciclo de periodo 10. A partir de este ciclo se buscó una regla de evolución que representara a un autómata celular (2,1). Por lo tanto se tomó el arreglo antes de iterarlo como la configuración inicial del autómata y se verificó el estado de evolución de cada una de las células centrales que conforman las vecindades de tamaño 3 en las secuencias generadas durante las iteraciones. De esta manera la regla obtenida es la 43, la cual reproduce el comportamiento del tránsito bajo el escenario planteado.

Una vez encontrada la regla de evolución se construyeron los diagramas aplicando la misma mecánica de análisis expuesta en los capítulos anteriores para conocer las características que posee la regla. De esta forma se construyó el diagrama de Bruijn el cual se muestra en la figura 5.4.

A partir del diagrama de Bruijn se construyó su diagrama de subconjuntos (ver figura 5.5) para saber si existen Jardines del Edén para esta regla, encontrando que la secuencia 111 es precisamente de este tipo, aspecto que parece ser desfavorable ya que al trabajar con un autómata celular (2,1) para modelar flujo de tránsito la naturaleza del mismo nos indica que solamente hay dos estados, 0 que representa un sitio desocupado y 1 que representa un sitio ocupado por un auto (igual que en la regla 184), de tal forma que hay una divergencia entre la regla 43 la cual solamente puede presentar la secuencia 111 en la configuración inicial y el modelo de Nagel el cual sí permite un grupo de tres autos situados consecutivamente.

Figura 5.5: Diagrama de subconjuntos de la regla 43.

Lo anterior puede ser un indicio de que la regla 43 no cumple por completo con los requerimientos para reproducir el tránsito de autos de manera equivalente al modelo de Nagel con 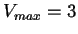$V_{max} = 3$. Para verificar lo anterior construimos los diagramas de Bruijn extendidos de los cuales se obtienen las secuencias que permiten ver los desplazamientos de las mismas con el fin de comprobar si coinciden éstos con los que se generan en el modelo original.

Figura 5.6: Diagrama de Bruijn de la regla 43 extendido a vecindades parciales de 4 células.

Como se ha mencionado anteriormente, de los diagramas de Bruijn se obtienen los ciclos que construyen secuencias que muestran diferentes desplazamientos a través de la evolución del autómata celular. Para comprobar si la regla 43 representa el comportamiento del mo-delo de Nagel para tránsito de autos en una dimensión tomemos el subdiagrama integrado por los nodos 1, 3, 7, 14, 12 y 8 (ver figura 5.8), el cual produce una secuencia que tiene un desplazamiento de sus células de dos posiciones a la izquierda en una generación. Si tomamos esa misma secuencia, la cual puede ser 000111 (o cualquier permutación de ésta) como una configuración donde los ceros representan espacios vacios y los unos espacios ocupados con una velocidad inicial 0 para todos los vehículos, tendremos como resultado que el desplazamiento no coincide con el de la secuencia producida por el subdiagrama ya que la secuencia 000111 se transforma en la secuencia 011100 en la siguiente generación mientras que aplicando el modelo de Nagel la configuración que se obtiene en el siguiente paso de tiempo es 1**00*, donde 1 representa un sitio ocupado por un vehículo con 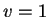$v = 1$, * representa un sitio desocupado y 0 representa un sitio ocupado por un auto con $v = 0$.

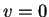Figura 5.7: Diagrama de Bruijn de la regla 43 extendido a vecindades parciales de 6 células.

Este tipo de aspectos se pueden observar en otros subdiagamas que representan otros desplazamientos y que hacen que la regla 43 no represente de manera global el mismo comportamiento que al aplicar a una configuración arbitraria el modelo de Nagel con 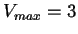$V_{max} = 3$. De hecho, estas inconsistencias se pueden observar desde las evoluciones mismas de las células centrales que conforman las vecindades. Por ejemplo, en la configuración inicial de la figura 5.3 se puede observar que la vecindad 100 evoluciona a 1 en la siguiente generación, siendo 1 el estado que representa un sitio ocupado por un auto sin tomar en cuenta velocidades, mientras que en las subsecuentes generaciones la vecindad 100 evoluciona a 0 tal y como lo indica la regla.

Figura 5.8: Desplazamientos en una generación que tienen las células al aplicar la regla de AC(2,1) 43.

Este, como otros detalles semejantes tienen varias explicaciones: la primera es que si en el estado global inicial asumimos que para todos los autos 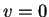$v = 0$, entonces por consecuencia aunque un auto tenga dos espacios vacios adelante de él sólo avanzará uno de acuerdo a los pasos del modelo de Nagel y no dos como lo indica la regla 43; la segunda explicación es que la regla sólo es consistente mientras 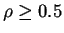$\rho \geq 0.5$, porque en el momento que 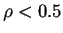$\rho < 0.5$ la regla se desajusta del funcionamiento de acuerdo al modelo de Nagel; la tercera explicación es que al ser la regla 43 un autómata binario, el reducir la densidad afecta debido a que el autómata sólamente contempla dos estados, los cuales no tienen nada que ver con las velocidades de los autos, mientras que en el modelo de Nagel el manejar 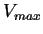$V_{max}$ con diferentes valores hace posible un mayor número de situaciones las cuales no puede incluir el autómata celular en cuestión debido a su propia naturaleza.