Autómatas Celulares Lineales con r=1/2

Antes de continuar con el análisis de autómatas reversibles, revisaremos, en especial, a los autómatas con radio de vecindad $r=1/2$. La finalidad es poder representar a todo autómata celular lineal de cualquier radio de vecindad como se muestra en los trabajos de Jarkko Kari [Kari 92] y de Tim Boykett [Boykett 97].

Supongamos que tenemos un autómata celular $(k,r)$ cuyo tamaño de vecindad es $2r+1$, para reducir este tamaño a $2$, aumentaremos el número de estados, de este modo, un autómata $(k^{2r},1/2)$, se puede utilizar para representar a la misma evolución, es decir, tomaremos del autómata general todas las posibles secuencias de tamaño $2r$ o lo que es lo mismo, todos los posibles nodos de de Bruijn [McIntosh 91a].

Sabemos que originalmente, para todo estado $e \in K$, sobre una secuencia de estados $S \in K^{2r+1}$ la regla de evolución original tiene el siguiente comportamiento:

$$\phi(S_0,\ldots,S_{2r}) \rightarrow e$$ (5.1)

Esta regla se aplica a cada célula en la configuración, ahora, para dicha configuración agrupemos sus celulas en secuencias de tamaño $2r$, obtendremos tantas secuencias distintas como $k^{2r}$ que serán nuestros nuevos estados, para cada par de estos nuevos elementos, la nueva regla de evolución funcionará de la siguiente manera:

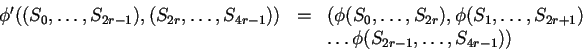$$\begin{array}{ccl} \phi'((S_0,\ldots,S_{2r-1}),(S_{2r},\ldot... ...r+1}) \\ && \ldots \phi(S_{2r-1},\ldots,S_{4r-1})) \end{array}$$ (5.2)

La nueva regla será el producto de aplicar repetidamente la regla original sobre dos secuencias de nuevos estados. Como producto de aplicar la regla original obtendremos una nueva secuencia de $2r$ elementos, es decir, un nodo de de Bruijn o una secuencia dentro del conjunto de nuevos estados.

Veamos como funciona esto en un autómata $(2,1)$ con regla $111$.

Tabla 5.1: Autómata $(2,1)$ regla $111$

$\begin{array}{ccccc} &00&01&10&11 \\ \cline{2-5} \multicolumn{1}{c\vert}{00}&... ...rt}{10}& 0&1 & & \\ \multicolumn{1}{c\vert}{11}& & & 1&0 \\ \end{array}$

Aplicando la regla de evolución al autómata a partir de la confiuración inicial se obtiene lo siguiente:

$$\begin{array}{rccccccccccccc} \mbox{Configuraci\'on Inicial}... ...\\ \mbox{Evoluci\'on}&\rightarrow&011110111111 \\ \end{array}$$

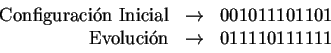
Tomemos ahora todas las posibles secuencias de tamaño $2r$ y renombremos estas para obtener un nuevo conjunto de estados.

Tabla 5.2: Renombrando las secuencias de tamaño $2$ con nuevos estados

Secuencia		Estado nuevo
00	$\rightarrow$	0
01	$\rightarrow$	1
10	$\rightarrow$	2
11	$\rightarrow$	3

De las cadenas de $2$ elementos, obtengamos su evolución al aplicar la regla original.

Tabla 5.3: Secuencias de tamaño $4$ y su evolución

0000 11	0001 11	0010 11	0011 11	0100 10	0101 11	0110 11	0111 10
1000 01	1001 01	1010 11	1011 11	1100 10	1101 11	1110 01	1111 00

Si agrupamos en bloques de tamaño $2r$ cada una de estas secuencias, lo que producirá es:

Tabla 5.4: Agrupación de las secuencias en bloque de tamaño $2$

Si sustituimos cada bloque por el estado nuevo asignado anteriormente obtendremos:

Tabla 5.5: Sustitución de los bloques de tamaño $2$ por los nuevos estados

La nueva regla $(4,1/2)$ que simula la evolución del autómata original es:

Tabla 5.6: Autómata $(4,1/2)$ que simula el comportamiento del autómata $(2,1)$

$\begin{array}{ccccc} &0&1&2&3 \\ \cline{2-5} \multicolumn{1}{c\vert}{0}& 3&3&... ...c\vert}{2}& 1&1&3&3 \\ \multicolumn{1}{c\vert}{3}& 2&3&1&0 \\ \end{array}$

Con la configuracion inicial que utilizamos al principio, hagamos con sus elementos secuencias de tamaño $k^{2r}=2^{(2*1/2)}=2$, cada una de estas secuencias se sustituirá por los estados nuevos cada secuencia. Después de aplicar la regla $(4,1/2)$ a esta nueva secuencia de símbolos, se regresa cada estado a la secuencia original de tamaño $2$.

Tabla 5.7: Secuencias de tamaño $2$ que evolucionan con la regla $(4,1/2)$

C.I.	$\rightarrow$
		0		2		3		2		3		1
	$\rightarrow$		3		3		1		3		3		2

De esta manera, reordenando las secuencias de $2$ elementos tenemos el funcionamiento original del autómata.

Tabla 5.8: Simulación del autómata $(2,1)$ por medio de la regla $(4,1/2)$

0	0	1	0	1	1	1	0	1	1	0	1
	1	1	1	1	0	1	1	1	1	1	1	0

$\downarrow$

0	0	1	0	1	1	1	0	1	1	0	1
0	1	1	1	1	0	1	1	1	1	1	1