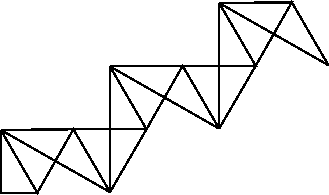


Next: First Level Triflexagon
Up: Trigonal Flexagons
Previous: Contents
Flexagons can become fairly complicated. The ones based on triangles are most conveniently made from long strips of paper; a roll of adding machine or calculator tape is ideal for this purpose given its convenient width. Crooked strips can be gotten by gluing faces of straight strips together, or just cutting out prepared segments and then joining them together. Leaving one extra triangle in each segment for overlapping and later gluing leads to efficient constructions.
Coloring the triangles is another problem, which can be done with crayons or markers once it is known which colors ought to be used. Aside from copying an already existent design, this is best done by drawing the Tukey triangles and then lettering or numbering the triangles in the strip. That information is sufficient to fold up the strip, since pairs of consecutive numbers are to be hidden by folding them together. Painting can be done before folding by following a color code for the numbers, or after the folding is done, when the faces can be painted wholesale, or even embellished with designs.
Making pages of cutouts, even the ones folded from ``straight'' strips, require a higher degree of preparation to fit them into the rectangular format of a page, although it is relatively easy to assemble a collection of primitive components which later can be glued together according to the necessities of the individual flexagon.
Although flexagons can be created from any convex polygon, the variety of possibilities to be explored is greatly reduced by using tringles. Even so, there are many possibilities to try out, but the following list shows up some of the more important regularities.
- 1.
- The classical flexagon is built from equilateral triangles, so that all thre angles are the same and equal to
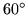 .
The plans of the homogeneous normal flexagons, with
.
The plans of the homogeneous normal flexagons, with
 triangles and
triangles and
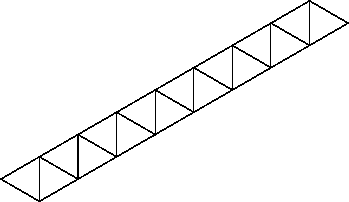
 faces, their genotypes are all straight strips as shown in Figure 1.
faces, their genotypes are all straight strips as shown in Figure 1.
Figure 1:
The classical flexagon.
 |
Because the angle between every triangle and its reflection will be the same 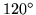 ,
the smallest combination which will fill out
,
the smallest combination which will fill out 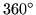 requires three sectors. Trying to make do with only two sectors will result in one flexacup or another, none of which can be flexed through a full cycle although they will offer different color combinations to view. Of course more than three sectors could be used, but such excessive flexagons are always rather ungainly.
requires three sectors. Trying to make do with only two sectors will result in one flexacup or another, none of which can be flexed through a full cycle although they will offer different color combinations to view. Of course more than three sectors could be used, but such excessive flexagons are always rather ungainly.
- 2.
- The next most classical flexagon is the one made from isosceles right triangles, meaning angles of
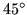 ,
,
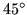 ,
and
,
and 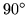 ,
its fame resting mostly on the flexatube.
,
its fame resting mostly on the flexatube.
Figure 2:
The flexatube precursor. One way to get the actual flexatube is to fill in the missing notches and work with diagonally creased squares.
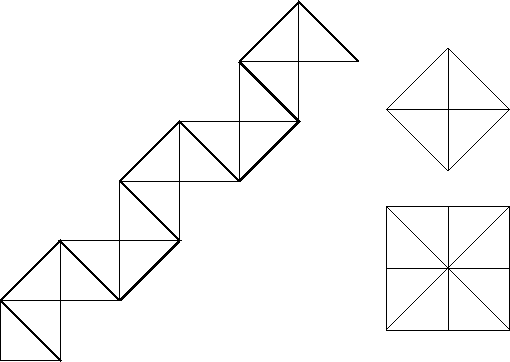 |
Depending on where the stack of triangles is opened, the sectorial angle can be either 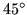 or
or 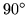 .
Two sectors of the formar will only make a flexacup; three sectors don't work very well, but four sectors will accomodate the
.
Two sectors of the formar will only make a flexacup; three sectors don't work very well, but four sectors will accomodate the 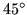 angles quite nicely. They show square phenotypes during two phases of the flexing cycle, with a third phase which can be skipped over by skipping a leaf during flexing and oscillating between the two flat forms.
angles quite nicely. They show square phenotypes during two phases of the flexing cycle, with a third phase which can be skipped over by skipping a leaf during flexing and oscillating between the two flat forms.
In the two-sector flexacup version, there is a temptation to place additional creases in the faces to obtain the flexatube configuration. Nevertheless, it doesn't quite work out, although it can be successfully performed, without any additional creasing, in the four-sector variant.
- 3.
- Half of an equilateral triangle is a skewed right triangle, having angles
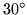 ,
,
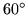 ,
and
,
and 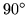 .
All three divide
.
All three divide 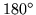 evenly and so will lie flat using six, three, or two sectors respectively. However, to avoid the flexacup phenomonon, the smallest angle needs to be accomodated, leading to a six-pointed star in the phenotype.
evenly and so will lie flat using six, three, or two sectors respectively. However, to avoid the flexacup phenomonon, the smallest angle needs to be accomodated, leading to a six-pointed star in the phenotype.
Figure 3:
The frieze which will fold up into a 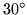 -
- 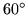 -
- 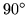 triagonal flexagon.
triagonal flexagon.
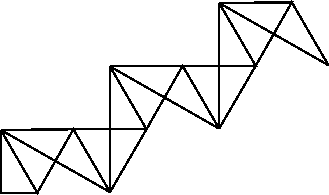 |
Two sectors will accomodate the 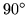 right triangle but the result is a flexacup which will not progress further. Likewise three sectors will permit the
right triangle but the result is a flexacup which will not progress further. Likewise three sectors will permit the 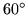 angles to surround the center and even allow a puckered arrangement of the
angles to surround the center and even allow a puckered arrangement of the 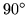 angles, but the best that can be done with the
angles, but the best that can be done with the 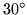 angles is to form a flexacup.
angles is to form a flexacup.
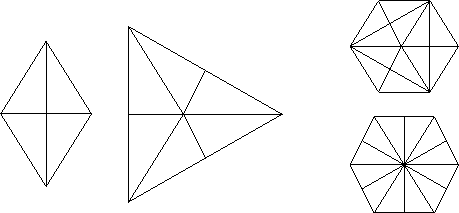
Figure 4:
Different phenotypes result from joining respectively two, three, or six sectors, each of which is shown in its planar phase.
 |
Although six sectors surround a center with 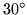 angles quite nicely, the space for the other vertices is quite cramped. By opening out every second leaf space can be made for the
angles quite nicely, the space for the other vertices is quite cramped. By opening out every second leaf space can be made for the 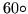 angles but there is still an excess of faces to get a strictly flat figure. However, some rearrangement of perimeter will produce another hexagonal figure which lies flat.
angles but there is still an excess of faces to get a strictly flat figure. However, some rearrangement of perimeter will produce another hexagonal figure which lies flat.
- 4.
- A third of an equilateral triangle is an obtuse isosceles triangle with angles
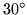 ,
,
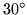 ,
and
,
and 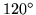 .
.
Figure 5:
With six sectors, there are two phases of the 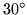 -
- 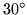 -
- 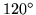 flexagon which will lie flat, the phenotype being a six-pointed star.
flexagon which will lie flat, the phenotype being a six-pointed star.
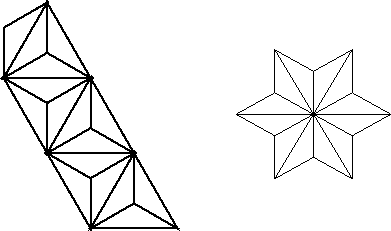 |
In this form the figure will lie flat during two phases of the flexing cycle.
- 5.
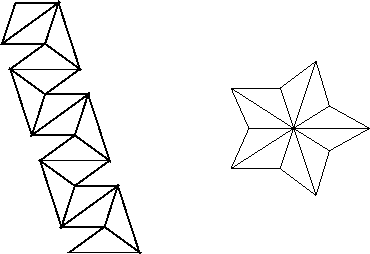
- Just to prove that it can be done, a five pointed phenotype can be constructed from an
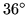 -
- 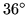 -
- 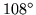 isosceles triangle.
isosceles triangle.
Figure 6:
By using angles of 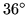 -
- 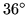 -
- 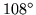 five sectors will produce a flat flexagon. Left: the genotypic plan as a frieze. Right: the resulting phenotype when the central angle is
five sectors will produce a flat flexagon. Left: the genotypic plan as a frieze. Right: the resulting phenotype when the central angle is 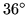 .
.
 |



Next: First Level Triflexagon
Up: Trigonal Flexagons
Previous: Contents
Microcomputadoras
2000-11-01
![]() ,
the smallest combination which will fill out
,
the smallest combination which will fill out ![]() requires three sectors. Trying to make do with only two sectors will result in one flexacup or another, none of which can be flexed through a full cycle although they will offer different color combinations to view. Of course more than three sectors could be used, but such excessive flexagons are always rather ungainly.
requires three sectors. Trying to make do with only two sectors will result in one flexacup or another, none of which can be flexed through a full cycle although they will offer different color combinations to view. Of course more than three sectors could be used, but such excessive flexagons are always rather ungainly.

![]() or
or ![]() .
Two sectors of the formar will only make a flexacup; three sectors don't work very well, but four sectors will accomodate the
.
Two sectors of the formar will only make a flexacup; three sectors don't work very well, but four sectors will accomodate the ![]() angles quite nicely. They show square phenotypes during two phases of the flexing cycle, with a third phase which can be skipped over by skipping a leaf during flexing and oscillating between the two flat forms.
angles quite nicely. They show square phenotypes during two phases of the flexing cycle, with a third phase which can be skipped over by skipping a leaf during flexing and oscillating between the two flat forms.
![]() right triangle but the result is a flexacup which will not progress further. Likewise three sectors will permit the
right triangle but the result is a flexacup which will not progress further. Likewise three sectors will permit the ![]() angles to surround the center and even allow a puckered arrangement of the
angles to surround the center and even allow a puckered arrangement of the ![]() angles, but the best that can be done with the
angles, but the best that can be done with the ![]() angles is to form a flexacup.
angles is to form a flexacup.

![]() angles quite nicely, the space for the other vertices is quite cramped. By opening out every second leaf space can be made for the
angles quite nicely, the space for the other vertices is quite cramped. By opening out every second leaf space can be made for the ![]() angles but there is still an excess of faces to get a strictly flat figure. However, some rearrangement of perimeter will produce another hexagonal figure which lies flat.
angles but there is still an excess of faces to get a strictly flat figure. However, some rearrangement of perimeter will produce another hexagonal figure which lies flat.