Teoría del campo promedio

La teoría del campo promedio se basa en que los elementos del conjunto de estados $K$ son independientes entre sí, es decir, no hay correlación en cada uno de los elementos que se encuentran en el espacio de evoluciones, bajo esta condición es fácil estimar la probabilidad de los estados en una vecindad en términos de la probabilidad de un solo estado (el estado al que evoluciona la vecindad). La probabilidad de la vecindad es el producto de las probabilidades de los estados que forman la vecindad.

La probabilidad de que una célula tenga un estado en particular en el tiempo $t+1$, es la suma de las probabilidades de las vecindades que se transforman a este estado en el tiempo $t$.

La vecindad está formada por $\mathcal V+1$ células, tomando la cardinalidad del conjunto de estados $\vert K\vert=k$, entonces la regla de evolución tiene $k^{\mathcal V+1}$ vecindades. La función de transición $\varphi({\mathbf{x}_{0}},\ldots,{\mathbf{x}_{\mathcal V}})$ se transformará en 0 ó 1 dependiendo de la suma de sus vecinos, cada una de las vecindades que existen en una regla de evolución se representarán como $X_{j}$, donde $j$ tomará valores de $0,\ldots,k^{\mathcal V+1}-1$.

Sea $p$ la probabilidad de tener el estado 1 en el tiempo $t$, su complemento o coprobabilidad $q=1-p$ es la probabilidad de tener el estado 0 en el tiempo $t$, $v$ es el número de veces que aparece el estado 1 en la vecindad, $n-v$ es el número de veces que aparece el estado 0 en la vecindad, la suma tomará cada una de las vecindades definidas por el conjunto $k^{\mathcal V+1}$, entonces la teoría del campo promedio calcula la densidad en el tiempo $t+1$ con el siguiente polinomio:

$$p_{t+1}=\sum_{j=0}^{k^{\mathcal V+1}-1}\varphi(X_{j}) p_{t}^{v} q_{t}^{n-v}.$$ (4)

Nótese que $k^{\mathcal V+1}$ es el número de vecindades y $K^{\mathcal V+1}$ es el conjunto que define cada una de las vecindades, además la teoría del campo promedio puede ser empleada en autómatas celulares de diferentes dimensiones. Los puntos fijos que calcula la teoría del campo promedio son una estimación de la densidad de los estados en un largo tiempo, además esta densidad es independiente de la densidad inicial.

La relación que existe entre la teoría del campo promedio y los polinomios de Bernstein se establece entre los polinomios de las Ecuaciones 3 y 4. La Ecuación 4 calcula todos los términos del polinomio, es decir, analiza todos los términos que genera la regla de evolución. Por otra parte el polinomio de Bernstein de la Ecuación 3 calcula todas las combinaciones que se pueden generar de un estado en una vecindad, esto produce un término del polinomio de la Ecuación 4 en específico para un $n$ y $v$ dado, donde $n$ tomará el valor $\mathcal V+1$ y $v$ el número de veces que un estado puede estar en la vecindad, es decir, $v$ tomará valores entre $0 \leq v \leq \mathcal V+1$.

Finalmente los polinomios de Bernstein ayudan a no calcular todos los términos posibles del polinomio del campo promedio. Simplemente calcula las combinaciones para un número de veces que estará un estado en la vecindad, excluyendo todos aquellos términos que no forman parte del polinomio.

Utilizando el polinomio del campo promedio y los polinomios de Bernstein, derivamos el polinomio del campo promedio que calcule la probabilidad de $p_{t+1}$ en reglas de evolución semitotalísticas de la siguiente manera:

$$p_{t+1} = \sum_{v=S_{min}}^{S_{max}} \left (\begin{array}{c} n-1 ... ...x}} \left (\begin{array}{c} n-1 \\ v \end{array} \right ) p_{t}^{v} q_{t}^{n-v}$$ (5)

donde $n$ representa el número de células que forman una vecindad, $n-1$ indica el número de vecinos en la vecindad, $v$ es el número de veces que aparece el estado 1 en la vecindad, $n-v$ es el número de veces que aparece el estado 0 en la vecindad, $p_{t}$ es la probabilidad de tener el estado 1, $q_{t}$ es la probabilidad de tener el estado 0, la combinatoria $\left (\begin{array}{c} n-1 \\ v \end{array} \right )$ 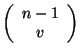calcula las constantes para cada uno de los términos del polinomio.

La primera suma de la Ecuación 5 calcula todas las combinaciones que se derivan del intervalo que definen $S_{min}$ y $S_{max}$ en el caso de la sobrevivencia, la segunda suma calcula todas las combinaciones que se derivan del intervalo que definen $N_{min}$ y $N_{max}$ en el caso de los nacimientos. En el caso de la sobrevivencia al exponente $v$ se le suma un elemento porque la célula central está viva, en el caso de los nacimientos no se le suma ningún elemento porque la célula central está muerta. El exponente $v$ para la variable $p_{t}$ se calcula sumando el número de células ocupadas por el estado 1 en la vecindad, el exponente $n-v$ para la variable $q$ se calcula sumando el número de células ocupadas por el estado 0 en la vecindad.

El polinomio de la Ecuación 5 no puede ser aplicado a reglas de evolución que no sean semitotalísticas o totalísticas, en ese caso se tiene que aplicar la Ecuación 4.

La teoría del campo promedio ha sido empleada en [SS78], [Hem85], [GVK87], [GV87], [Gut89], [McI90], [CM92] y [Jua00], para tratar de explicar el comportamiento de los estados en el espacio de evoluciones, la mayoría de estos estudios describen el comportamiento de las células a través de su densidad a través del tiempo. Este análisis propone un enfoque sencillo y práctico de como obtener dichas densidades e interpretar fácilmente los resultados, tal como lo plantean McIntosh en [McI90] y Chaté-Manneville en [CM92], graficando su curva de probabilidad en el tiempo inicial y calculando sus curvas de probabilidad a través del tiempo, sustituyendo el polinomio de la Equación 5 de manera iterativa. La teoría del campo promedio es un modelo simple que proporciona propiedades estadísticas de los autómatas celulares.