Homomorphisms
A mapping from the nodes of one graph to those of another which preserves linkages is called a homomorphism, whose definition was already introduced while defining the ordering of graphs. In short, the larger graph is a homomorphic image of the smaller, even though the scarcity of its nodes will run counter to this intuition.
However, there is a subtle point which concerns the mappings of non-links --- should they also be respected? As stated, the definition allows a single node linked to itself to be the maximum of all graphs; the requisite mapping is simply a constant mapping. All images are thereby linked, even when their counterimages are not. Another instance where the difference is felt concerns the difference between equivalence relations and congruence relations.
Equivalence classes are the constant value contours of functions; congruence classes are contours of homomorphisms. It might be interesting to impose a uniformity requirement, such as stipulating that 0.4em
In other words, links would always have to be uniform throughout congruence classes, but a moment's thought shows that this need not even be true for all cartesian products, where one would surely expect such a result to be valid. Uniformity would disallow too many reasonable non-links; if non-links as well as links had to be preserved, this congruence relation would characterize such a homomorphism.
A graph of the sort required, where every member of a set of p elements is
linked to all the members of a set of q elements is traditionally named 
; 
is simply 
.
As homomorphisms have been defined, the only requirement which two congruence classes have to satisfy is that if their images are linked, at least one pair of representatives have to be linked; this is still enough of a requirement to distinguish between equivalences and congruences. Let P and Q be congruence classes; then
The discarded version would have read:
A new diagram constructed from the congruence classes of another will have fewer nodes, still preserving the links of the original diagram. Such replacements are often sought, in the interest of economy. In the extreme case of a maximum congruence relation, the final graph will have a minimum number of nodes, a unique representation of the original diagram and all others homomorphic to it.
Consider again the intersection of two diagrams, while supposing that 
means that b=d and that link
means link
with respect to
equivalence classes. Then the projection 
is a
mapping from the intersection to its second factor whose equivalence classes correspond to
the first factor; there is a similar projection 
for the first factor. Either is a congruence relation because the mapping is defined
uniformly for the entire equivalence class. Figure 4
illustrates this relationship.
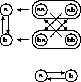
Figure 4: Congruence classes for the projection of a cartesian product
onto its second coordinate; vertical components of links are respected.
Note that there are no links within a single congruence class, as a consequence of which there are no self-loops in the projection.
Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx