Hamiltonian and Eulerian paths
Hamiltonian paths in a diagram are those which visit each vertex once and only once; Hamiltonian loops are those for which the tour returns to the starting point. In contrast Eulerian paths are those which use every edge in the diagram once and only once, loops likewise completing a circuit by returning to the start.
An Eulerian problem, to decide whether such paths exist or not, is readily soluble; for loops, each vertex must have as many incoming as outgoing links, and the diagram as a whole must be connected (which is certainly true of a de Bruijn diagram). For paths, the terminal nodes could be separated, allowing one extra outgoing link at the initial node plus a surplus incoming link at the terminal node. Euler's classical result refers to undirected links; I. J. Good [14] proved the analogous directed variant in 1946.
A Hamiltonian problem is usually intractable, but for de Bruijn diagrams, the dual of a diagram of n stages is the diagram of n+1 stages. Consequently, running through all the links in any diagram is equivalent to running through all the nodes of its successor, allowing the Eulerian result to solve the equivalent Hamiltonian problem for an additional stage.
Demonstrating existence is much easier than counting, in turn simpler than exhibiting, paths. In 1946 N. J. de Bruijn [15] obtained a recursion relation to count the Hamiltonian paths in a binary diagram exploiting duality, which he called doubling; a sufficiently significant result to associate his name with the graph. Additional discussion can be found in Marshall Hall, Jr.,'s Combinatorial Theory [16].
When diagrams are both Hamiltonian and Eulerian, every Hamiltonian circuit can be promoted to an Eulerian circuit and the interesting question is to determine in how many ways. Shift register theory esteems the actual sequences highly; a good part of Golomb's book [7] concentrates on obtaining them. Automata theory is less concerned with this particular detail, but it is still useful to know some procedures.
An upper bound on the number of Hamiltonian cycles is always that number of cycles
whose length matches the number of nodes. Since the diagram of order n has 
nodes, by Eq. 21 this
number is 
. For binary diagrams, de Bruijn's
value is 
. Aside from number theoretic
deformations at low values of n, comparison of the results would lead one to
believe that 
of all candidates are Hamiltonian.
Similarly, the number of loops whose length equals the total number of links bounds the number of Eulerian cycles; in both cases, degenerate loops must be discounted to get the true count.
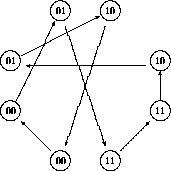
Figure 12: A Hamiltonian path in the (2,3/2) de Bruijn diagram.
Figure 12 illustrates several of the points which have
been discussed; it shows one of the two Hamiltonian paths associated with the matrix 
, but the nodes have been labelled according to 
. Homomorphism is apparent---the numerical node
indices have been reduced modulo 4, while the residues modulo 2 (linkages) have not
changed. If duplicate nodes were superimposed and reference made to Figure 7, one of the Eulerian loops of the latter would manifest
itself; a Hamiltonian path wrapped around the image twice.
There is an embedment in the opposite direction too---the 
diagram fits into just half of the 
diagram. All the arrows are there; homomorphism fails when they don't
all close up within the image of 
itself, the
trick is to match up two copies of the image to get the next diagram. In fact, when this
arrangement presents itself one should always try to arrange an inverse homomorphism.
Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx