Order relation

Consequently a more general point of view might hold that the larger graph contains all the paths of the smaller, especially the loops. Actually, the image of a loop has to be a loop because any point of closure has the same image as the point of departure; but additional loops may exist in the image. To repeat, we want to say that a larger graph has more paths, even if they are degenerate; such a viewpoint is still consistent with embedment into a graph that the first sense considers larger.

Consider (writing ab for (a,b) whenever it is unambiguous to improve legibility)

and

these graphs are diagrammed in Figure 1.

 
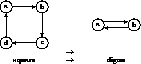
Figure 1: A digon is larger than a square, which has no loops of length 2.  

The second, larger, is a digon with its vertices linked to one another; the first, smaller, is a square with successive vertices linked. Mapping a to a, b to b, c to a, and d to b, it is seen that cycles around the square runs twice around the digon, with similar relationships for other paths.

The interesting point is that the larger is not a superset of the larger, but rather it contains a functional image. One might say that means that there exists a function such that

This definition reduces to the previous one when f is the injection map that inserts a subset into the set containing it, but allows a comparison which extends far beyond pairs of diagrams in which one is a subset of the other.

Strictly, it must be proved that this general comparison is an order relation. The only complicated point is proving antisymmetry, that when and (and links are conserved), X and Y are at least equivalent if not identical. The mapping applied in succession to the integers, even integers, and the multiples of four shows that this need not be true in general, although it works out well enough for finite sets.

---

Harold V. McIntosh
E-mail:mcintosh@servidor.unam.mx